
作者 | 我被狗咬了
來源 | 亂燉
生活中我們經常會遇到一些加密算法,今天我們就聊聊這些加密算法的實現。部分常用的加密方法基本都有對應的庫,基本不再需要我們用代碼實現具體算法
MD5加密
全稱:MD5消息摘要算法(英語:MD5 - ),一種被廣泛使用的密碼散列函數,可以產生出一個128位(16字節)的散列值(hash value),用于確保信息傳輸完整一致。md5加密算法是不可逆的,所以解密一般都是通過暴力窮舉方法,通過網站的接口實現解密。代碼:
import?hashlib
m?=?hashlib.md5()
m.update(str.encode("utf8"))
print(m.hexdigest())SHA1加密
全稱:安全哈希算法( Hash )主要適用于數字簽名標準( DSS)里面定義的數字簽名算法( DSA),SHA1比MD5的安全性更強。對于長度小于2^ 64位的消息常用的對稱密碼算法有哪些,SHA1會產生一個160位的消息摘要。代碼:
import hashlib
sha1?=?hashlib.sha1()
data?=?'2333333'
sha1.update(data.encode('utf-8'))
sha1_data?=?sha1.hexdigest()
print(sha1_data)
HMAC加密
全稱:散列消息鑒別碼(Hash Code),HMAC加密算法是一種安全的基于加密hash函數和共享密鑰的消息認證協議。實現原理是用公開函數和密鑰產生一個固定長度的值作為認證標識,用這個標識鑒別消息的完整性。使用一個密鑰生成一個固定大小的小數據塊,即 MAC,并將其加入到消息中,然后傳輸。接收方利用與發送方共享的密鑰進行鑒別認證等。代碼:
import?hmac
import?hashlib
#?第一個參數是密鑰key,第二個參數是待加密的字符串,第三個參數是hash函數
mac?=?hmac.new('key','hello',hashlib.md5)
mac.digest()??#?字符串的ascii格式
mac.hexdigest()??#?加密后字符串的十六進制格式
DES加密
全稱:數據加密標準(Data ),屬于對稱加密算法。DES是一個分組加密算法,典型的DES以64位為分組對數據加密,加密和解密用的是同一個算法。它的密鑰長度是56位(因為每個第8 位都用作奇偶校驗),密鑰可以是任意的56位的數,而且可以任意時候改變。代碼:

import?binascii
from?pyDes?import?des,?CBC,?PAD_PKCS5
#?需要安裝?pip?install?pyDes
def?des_encrypt(secret_key,?s):
????iv?=?secret_key
????k?=?des(secret_key,?CBC,?iv,?pad=None,?padmode=PAD_PKCS5)
????en?=?k.encrypt(s,?padmode=PAD_PKCS5)
????return?binascii.b2a_hex(en)
def?des_decrypt(secret_key,?s):
????iv?=?secret_key
????k?=?des(secret_key,?CBC,?iv,?pad=None,?padmode=PAD_PKCS5)
????de?=?k.decrypt(binascii.a2b_hex(s),?padmode=PAD_PKCS5)
????return?de
secret_str?=?des_encrypt('12345678',?'I?love?YOU~')
print(secret_str)
clear_str?=?des_decrypt('12345678',?secret_str)
print(clear_str)AES加密
全稱:高級加密標準(英語: ),在密碼學中又稱加密法,是美國聯邦政府采用的一種區塊加密標準。這個標準用來替代原先的DES,已經被多方分析且廣為全世界所使用。代碼:
import?base64
from?Crypto.Cipher?import?AES
'''
AES對稱加密算法
'''
#?需要補位,str不是16的倍數那就補足為16的倍數
def?add_to_16(value):
????while?len(value)?%?16?!=?0:
????????value?+=?'\0'
????return?str.encode(value)??#?返回bytes
#?加密方法
def?encrypt(key,?text):
????aes?=?AES.new(add_to_16(key),?AES.MODE_ECB)??#?初始化加密器
????encrypt_aes?=?aes.encrypt(add_to_16(text))??#?先進行aes加密
????encrypted_text?=?str(base64.encodebytes(encrypt_aes),?encoding='utf-8')??#?執行加密并轉碼返回bytes
????return?encrypted_text
#?解密方法
def?decrypt(key,?text):
????aes?=?AES.new(add_to_16(key),?AES.MODE_ECB)??#?初始化加密器
????base64_decrypted?=?base64.decodebytes(text.encode(encoding='utf-8'))??#?優先逆向解密base64成bytes
????decrypted_text?=?str(aes.decrypt(base64_decrypted),?encoding='utf-8').replace('\0',?'')??#?執行解密密并轉碼返回str
????return?decrypted_textRSA加密

全稱:--,RSA加密算法是一種非對稱加密算法。在公開密鑰加密和電子商業中RSA被廣泛使用。它被普遍認為是目前最優秀的公鑰方案之一。RSA是第一個能同時用于加密和數字簽名的算法,它能夠抵抗到目前為止已知的所有密碼攻擊。代碼:
#?-*-?coding:?UTF-8?-*-
#?reference?codes:?https://www.jianshu.com/p/7a4645691c68
import?base64
import?rsa
from?rsa?import?common
#?使用?rsa庫進行RSA簽名和加解密
class?RsaUtil(object):
????PUBLIC_KEY_PATH?=?'xxxxpublic_key.pem'??#?公鑰
????PRIVATE_KEY_PATH?=?'xxxxxprivate_key.pem'??#?私鑰
????#?初始化key
????def?__init__(self,
?????????????????company_pub_file=PUBLIC_KEY_PATH,
?????????????????company_pri_file=PRIVATE_KEY_PATH):
????????if?company_pub_file:
????????????self.company_public_key?=?rsa.PublicKey.load_pkcs1_openssl_pem(open(company_pub_file).read())
????????if?company_pri_file:
????????????self.company_private_key?=?rsa.PrivateKey.load_pkcs1(open(company_pri_file).read())
????def?get_max_length(self,?rsa_key,?encrypt=True):
????????"""加密內容過長時?需要分段加密?換算每一段的長度.
????????????:param?rsa_key:?鑰匙.
????????????:param?encrypt:?是否是加密.
????????"""
????????blocksize?=?common.byte_size(rsa_key.n)
????????reserve_size?=?11??#?預留位為11
????????if?not?encrypt:??#?解密時不需要考慮預留位
????????????reserve_size?=?0
????????maxlength?=?blocksize?-?reserve_size
????????return?maxlength
????#?加密?支付方公鑰
????def?encrypt_by_public_key(self,?message):
????????"""使用公鑰加密.
????????????:param?message:?需要加密的內容.
????????????加密之后需要對接過進行base64轉碼
????????"""
????????encrypt_result?=?b''
????????max_length?=?self.get_max_length(self.company_public_key)
????????while?message:
????????????input?=?message[:max_length]
????????????message?=?message[max_length:]
????????????out?=?rsa.encrypt(input,?self.company_public_key)
????????????encrypt_result?+=?out
????????encrypt_result?=?base64.b64encode(encrypt_result)
????????return?encrypt_result
????def?decrypt_by_private_key(self,?message):
????????"""使用私鑰解密.
????????????:param?message:?需要加密的內容.
????????????解密之后的內容直接是字符串,不需要在進行轉義
????????"""
????????decrypt_result?=?b""
????????max_length?=?self.get_max_length(self.company_private_key,?False)
????????decrypt_message?=?base64.b64decode(message)
????????while?decrypt_message:
????????????input?=?decrypt_message[:max_length]
????????????decrypt_message?=?decrypt_message[max_length:]
????????????out?=?rsa.decrypt(input,?self.company_private_key)
????????????decrypt_result?+=?out
????????return?decrypt_result
????#?簽名?商戶私鑰?base64轉碼
????def?sign_by_private_key(self,?data):
????????"""私鑰簽名.
????????????:param?data:?需要簽名的內容.
????????????使用SHA-1?方法進行簽名(也可以使用MD5)
????????????簽名之后,需要轉義后輸出
????????"""
????????signature?=?rsa.sign(str(data),?priv_key=self.company_private_key,?hash='SHA-1')
????????return?base64.b64encode(signature)
????def?verify_by_public_key(self,?message,?signature):
????????"""公鑰驗簽.
????????????:param?message:?驗簽的內容.
????????????:param?signature:?對驗簽內容簽名的值(簽名之后,會進行b64encode轉碼,所以驗簽前也需轉碼).
????????"""
????????signature?=?base64.b64decode(signature)
????????return?rsa.verify(message,?signature,?self.company_public_key)
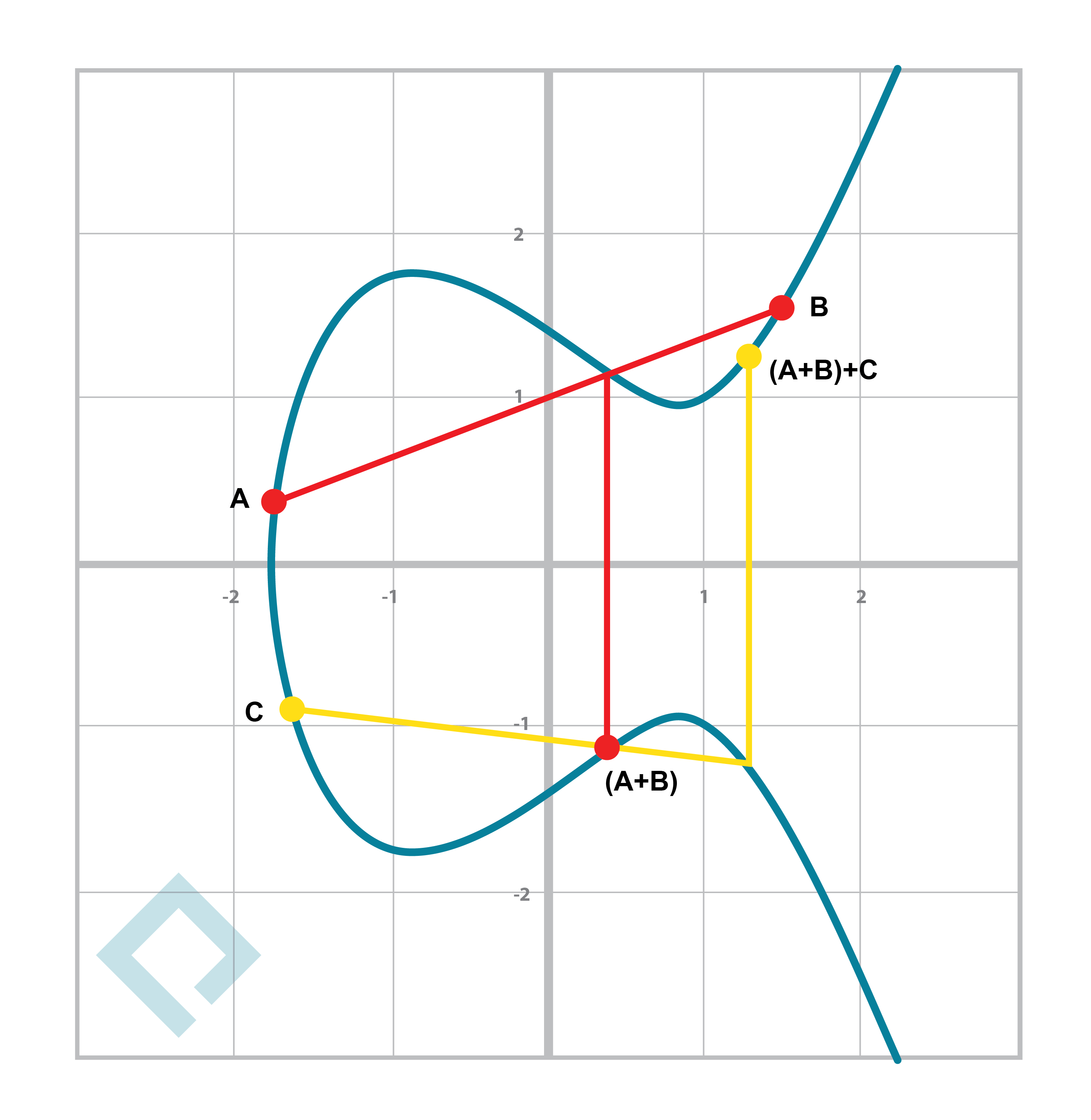
ECC加密
全稱:橢圓曲線加密( Curve )常用的對稱密碼算法有哪些,ECC加密算法是一種公鑰加密技術,以橢圓曲線理論為基礎。利用有限域上橢圓曲線的點構成的Abel群離散對數難解性,實現加密、解密和數字簽名。將橢圓曲線中的加法運算與離散對數中的模乘運算相對應,就可以建立基于橢圓曲線的對應密碼體制。代碼:
#?-*-?coding:utf-8?*-
#?author:?DYBOY
#?reference?codes:?https://blog.dyboy.cn/websecurity/121.html
#?description:?ECC橢圓曲線加密算法實現
"""
????考慮K=kG ,其中K、G為橢圓曲線Ep(a,b)上的點,n為G的階(nG=O∞?),k為小于n的整數。
????則給定k和G,根據加法法則,計算K很容易但反過來,給定K和G,求k就非常困難。
????因為實際使用中的ECC原則上把p取得相當大,n也相當大,要把n個解點逐一算出來列成上表是不可能的。
????這就是橢圓曲線加密算法的數學依據
????點G稱為基點(base?point)
????k(k
"""
def?get_inverse(mu,?p):
????"""
????獲取y的負元
????"""
????for?i?in?range(1,?p):
????????if?(i*mu)%p?==?1:
????????????return?i
????return?-1
def?get_gcd(zi,?mu):
????"""
????獲取最大公約數
????"""
????if?mu:
????????return?get_gcd(mu,?zi%mu)
????else:
????????return?zi
def?get_np(x1,?y1,?x2,?y2,?a,?p):
????"""
????獲取n*p,每次+p,直到求解階數np=-p
????"""
????flag?=?1??#?定義符號位(+/-)
????#?如果?p=q??k=(3x2+a)/2y1mod?p
????if?x1?==?x2?and?y1?==?y2:
????????zi?=?3?*?(x1?**?2)?+?a??#?計算分子??????【求導】
????????mu?=?2?*?y1????#?計算分母
????#?若P≠Q,則k=(y2-y1)/(x2-x1)?mod?p
????else:
????????zi?=?y2?-?y1
????????mu?=?x2?-?x1
????????if?zi*?mu?0:
????????????flag?=?0????????#?符號0為-(負數)
????????????zi?=?abs(zi)
????????????mu?=?abs(mu)
????#?將分子和分母化為最簡
????gcd_value?=?get_gcd(zi,?mu)?????#?最大公約數
????zi?=?zi?//?gcd_value????????????#?整除
????mu?=?mu?//?gcd_value
????#?求分母的逆元??逆元:??a ∈G ,ョb∈G 使得 ab = ba = e
????#?P(x,y)的負元是?(x,-y?mod?p)=?(x,p-y)?,有P+(-P)=?O∞
????inverse_value?=?get_inverse(mu,?p)
????k?=?(zi?*?inverse_value)
????if?flag?==?0:???????????????????#?斜率負數?flag==0
????????k?=?-k
????k?=?k?%?p
????#?計算x3,y3?P+Q
????"""
????????x3≡k2-x1-x2(mod?p)
????????y3≡k(x1-x3)-y1(mod?p)
????"""
????x3?=?(k?**?2?-?x1?-?x2)?%?p
????y3?=?(k?*?(x1?-?x3)?-?y1)?%?p
????return?x3,y3
def?get_rank(x0,?y0,?a,?b,?p):
????"""
????獲取橢圓曲線的階
????"""
????x1?=?x0?????????????#-p的x坐標
????y1?=?(-1*y0)%p??????#-p的y坐標
????tempX?=?x0
????tempY?=?y0
????n?=?1
????while?True:
????????n?+=?1
????????#?求p+q的和,得到n*p,直到求出階
????????p_x,p_y?=?get_np(tempX,?tempY,?x0,?y0,?a,?p)
????????#?如果?==?-p,那么階數+1,返回
????????if?p_x?==?x1?and?p_y?==?y1:
????????????return?n+1
????????tempX?=?p_x
????????tempY?=?p_y
def?get_param(x0,?a,?b,?p):
????"""
????計算p與-p
????"""
????y0?=?-1
????for?i?in?range(p):
????????#?滿足取模約束條件,橢圓曲線Ep(a,b),p為質數,x,y∈[0,p-1]
????????if?i**2%p?==?(x0**3?+?a*x0?+?b)%p:
????????????y0?=?i
????????????break
????#?如果y0沒有,返回false
????if?y0?==?-1:
????????return?False
????#?計算-y(負數取模)
????x1?=?x0
????y1?=?(-1*y0)?%?p
????return?x0,y0,x1,y1
def?get_graph(a,?b,?p):
????"""
????輸出橢圓曲線散點圖
????"""
????x_y?=?[]
????#?初始化二維數組
????for?i?in?range(p):
????????x_y.append(['-'?for?i?in?range(p)])
????for?i?in?range(p):
????????val?=get_param(i,?a,?b,?p)??#?橢圓曲線上的點
????????if(val?!=?False):
????????????x0,y0,x1,y1?=?val
????????????x_y[x0][y0]?=?1
????????????x_y[x1][y1]?=?1
????print("橢圓曲線的散列圖為:")
????for?i?in?range(p):??????????????#?i=?0->?p-1
????????temp?=?p-1-i????????#?倒序
????????#?格式化輸出1/2位數,y坐標軸
????????if?temp?>=?10:
????????????print(temp,?end="?")
????????else:
????????????print(temp,?end="??")
????????#?輸出具體坐標的值,一行
????????for?j?in?range(p):
????????????print(x_y[j][temp],?end="??")
????????print("")???#換行
????#?輸出?x?坐標軸
????print("??",?end="")
????for?i?in?range(p):
????????if?i?>=10:
????????????print(i,?end="?")
????????else:
????????????print(i,?end="??")
????print('\n')
def?get_ng(G_x,?G_y,?key,?a,?p):
????"""
????計算nG
????"""
????temp_x?=?G_x
????temp_y?=?G_y
????while?key?!=?1:
????????temp_x,temp_y?=?get_np(temp_x,temp_y,?G_x,?G_y,?a,?p)
????????key?-=?1
????return?temp_x,temp_y
def?ecc_main():
????while?True:
????????a?=?int(input("請輸入橢圓曲線參數a(a>0)的值:"))
????????b?=?int(input("請輸入橢圓曲線參數b(b>0)的值:"))
????????p?=?int(input("請輸入橢圓曲線參數p(p為素數)的值:"))???#用作模運算
????????#?條件滿足判斷
????????if?(4*(a**3)+27*(b**2))%p?==?0:
????????????print("您輸入的參數有誤,請重新輸入!!!\n")
????????else:
????????????break
????#?輸出橢圓曲線散點圖
????get_graph(a,?b,?p)
????#?選點作為G點
????print("user1:在如上坐標系中選一個值為G的坐標")
????G_x?=?int(input("user1:請輸入選取的x坐標值:"))
????G_y?=?int(input("user1:請輸入選取的y坐標值:"))
????#?獲取橢圓曲線的階
????n?=?get_rank(G_x,?G_y,?a,?b,?p)
????#?user1生成私鑰,小key
????key?=?int(input("user1:請輸入私鑰小key(<{}):".format(n)))
????#?user1生成公鑰,大KEY
????KEY_x,kEY_y?=?get_ng(G_x,?G_y,?key,?a,?p)
????#?user2階段
????#?user2拿到user1的公鑰KEY,Ep(a,b)階n,加密需要加密的明文數據
????#?加密準備
????k?=?int(input("user2:請輸入一個整數k(<{})用于求kG和kQ:".format(n)))
????k_G_x,k_G_y?=?get_ng(G_x,?G_y,?k,?a,?p)?????????????????????????#?kG
????k_Q_x,k_Q_y?=?get_ng(KEY_x,?kEY_y,?k,?a,?p)?????????????????????#?kQ
????#?加密
????plain_text?=?input("user2:請輸入需要加密的字符串:")
????plain_text?=?plain_text.strip()
????#plain_text = int(input("user1:請輸入需要加密的密文:"))
????c?=?[]
????print("密文為:",end="")
????for?char?in?plain_text:
????????intchar?=?ord(char)
????????cipher_text?=?intchar*k_Q_x
????????c.append([k_G_x,?k_G_y,?cipher_text])
????????print("({},{}),{}".format(k_G_x,?k_G_y,?cipher_text),end="-")
????#?user1階段
????#?拿到user2加密的數據進行解密
????#?知道?k_G_x,k_G_y,key情況下,求解k_Q_x,k_Q_y是容易的,然后plain_text?=?cipher_text/k_Q_x
????print("\nuser1解密得到明文:",end="")
????for?charArr?in?c:
????????decrypto_text_x,decrypto_text_y?=?get_ng(charArr[0],?charArr[1],?key,?a,?p)
????????print(chr(charArr[2]//decrypto_text_x),end="")
if?__name__?==?"__main__":
????print("*************ECC橢圓曲線加密*************")
????ecc_main()
本文主要介紹了MD5,SHA-1,HMAC,DES/AES,RSA和ECC這幾種加密算法和代碼示例。
END