
背包問題是一類經典的動態規劃問題,它非常靈活,需要仔細琢磨體會,本文先對背包問題的幾種常見類型作一個總結,然后再看看上幾個相關題目。
本文首發于我的博客,傳送門
根據維基百科,背包問題( )是一種組合優化的NP完全(NP-,NPC)問題。問題可以描述為:給定一組物品,每種物品都有自己的重量和價格,在限定的總重量內,我們如何選擇,才能使得物品的總價格最高。NPC問題是沒有多項式時間復雜度的解法的,但是利用動態規劃,我們可以以偽多項式時間復雜度求解背包問題。一般來講,背包問題有以下幾種分類:
01背包問題完全背包問題多重背包問題
此外,還存在一些其他考法,例如恰好裝滿、求方案總數、求所有的方案等。本文接下來就分別討論一下這些問題。
1. 01背包1.1 題目
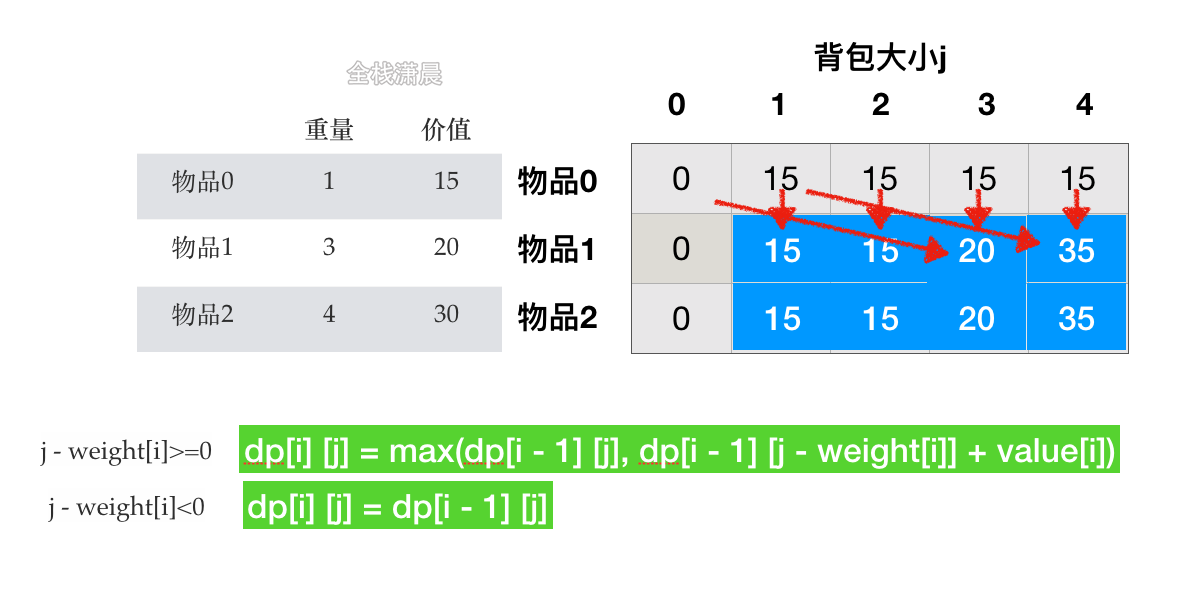
最基本的背包問題就是01背包問題(01 ):一共有N件物品,第i(i從1開始)件物品的重量為w[i],價值為v[i]。在總重量不超過背包承載上限W的情況下,能夠裝入背包的最大價值是多少?
1.2 分析
如果采用暴力窮舉的方式,每件物品都存在裝入和不裝入兩種情況,所以總的時間復雜度是O(2^N),這是不可接受的。而使用動態規劃可以將復雜度降至O(NW)。我們的目標是書包內物品的總價值,而變量是物品和書包的限重,所以我們可定義狀態dp:
dp[i][j]表示將前i件物品裝進限重為j的背包可以獲得的最大價值, 0<=i<=N, 0<=j<=W那么我們可以將dp[0][0...W]初始化為0,表示將前0個物品(即沒有物品)裝入書包的最大價值為0。那么當 i > 0 時dp[i][j]有兩種情況:
不裝入第i件物品,即dp[i?1][j];裝入第i件物品(前提是能裝下),即dp[i?1][j?w[i]] + v[i]。
即狀態轉移方程為
dp[i][j] = max(dp[i?1][j], dp[i?1][j?w[i]]+v[i]) // j >= w[i]由上述狀態轉移方程可知,dp[i][j]的值只與dp[i-1][0,...,j-1]有關,所以我們可以采用動態規劃常用的方法(滾動數組)對空間進行優化(即去掉dp的第一維)。需要注意的是,為了防止上一層循環的dp[0,...,j-1]被覆蓋,循環的時候 j 只能逆向枚舉(空間優化前沒有這個限制),偽代碼為:
// 01背包問題偽代碼(空間優化版)
dp[0,...,W] = 0
for i = 1,...,N
for j = W,...,w[i] // 必須逆向枚舉!!!
dp[j] = max(dp[j], dp[j?w[i]]+v[i])時間復雜度為O(NW), 空間復雜度為O(W)。由于W的值是W的位數的冪,所以這個時間復雜度是偽多項式時間。
動態規劃的核心思想避免重復計算在01背包問題中體現得淋漓盡致。第i件物品裝入或者不裝入而獲得的最大價值完全可以由前面i-1件物品的最大價值決定,暴力枚舉忽略了這個事實。
2. 完全背包2.1 題目
完全背包( )與01背包不同就是每種物品可以有無限多個:一共有N種物品,每種物品有無限多個,第i(i從1開始)種物品的重量為w[i],價值為v[i]。在總重量不超過背包承載上限W的情況下,能夠裝入背包的最大價值是多少?
2.2 分析一
我們的目標和變量和01背包沒有區別,所以我們可定義與01背包問題幾乎完全相同的狀態dp:
dp[i][j]表示將前i種物品裝進限重為j的背包可以獲得的最大價值, 0<=i<=N, 0<=j<=W初始狀態也是一樣的,我們將dp[0][0...W]初始化為0完全背包問題算法,表示將前0種物品(即沒有物品)裝入書包的最大價值為0。那么當 i > 0 時dp[i][j]也有兩種情況:
不裝入第i種物品,即dp[i?1][j],同01背包;裝入第i種物品,此時和01背包不太一樣,因為每種物品有無限個(但注意書包限重是有限的),所以此時不應該轉移到dp[i?1][j?w[i]]而應該轉移到dp[i][j?w[i]],即裝入第i種商品后還可以再繼續裝入第種商品。
所以狀態轉移方程為
dp[i][j] = max(dp[i?1][j], dp[i][j?w[i]]+v[i]) // j >= w[i]
這個狀態轉移方程與01背包問題唯一不同就是max第二項不是dp[i-1]而是dp[i]。
和01背包問題類似,也可進行空間優化,優化后不同點在于這里的 j 只能正向枚舉而01背包只能逆向枚舉,因為這里的max第二項是dp[i]而01背包是dp[i-1],即這里就是需要覆蓋而01背包需要避免覆蓋。所以偽代碼如下:
// 完全背包問題思路一偽代碼(空間優化版)
dp[0,...,W] = 0
for i = 1,...,N
for j = w[i],...,W // 必須正向枚舉!!!
dp[j] = max(dp[j], dp[j?w[i]]+v[i])由上述偽代碼看出,01背包和完全背包問題此解法的空間優化版解法唯一不同就是前者的 j 只能逆向枚舉而后者的 j 只能正向枚舉,這是由二者的狀態轉移方程決定的。此解法時間復雜度為O(NW), 空間復雜度為O(W)。
2.3 分析二
除了分析一的思路外,完全背包還有一種常見的思路,但是復雜度高一些。我們從裝入第 i 種物品多少件出發,01背包只有兩種情況即取0件和取1件,而這里是取0件、1件、2件...直到超過限重(k > j/w[i]),所以狀態轉移方程為:
# k為裝入第i種物品的件數, k <= j/w[i]
dp[i][j] = max{(dp[i-1][j ? k*w[i]] + k*v[i]) for every k}同理也可以進行空間優化,需要注意的是,這里max里面是dp[i-1],和01背包一樣,所以 j 必須逆向枚舉,優化后偽代碼為
// 完全背包問題思路二偽代碼(空間優化版)
dp[0,...,W] = 0
for i = 1,...,N
for j = W,...,w[i] // 必須逆向枚舉!!!
for k = [0, 1,..., j/w[i]]
dp[j] = max(dp[j], dp[j?k*w[i]]+k*v[i])相比于分析一,此種方法不是在O(1)時間求得dp[i][j],所以總的時間復雜度就比分析一大些了,為 O(NW \frac W {\bar{w}})級別。
2.4 分析三、轉換成01背包
01背包問題是最基本的背包問題,我們可以考慮把完全背包問題轉化為01背包問題來解:將一種物品轉換成若干件只能裝入0件或者1件的01背包中的物品。
最簡單的想法是,考慮到第 i 種物品最多裝入 W/w[i] 件,于是可以把第 i 種物品轉化為 W/w[i] 件費用及價值均不變的物品,然后求解這個01背包問題。
更高效的轉化方法是采用二進制的思想:把第 i 種物品拆成重量為 w_i 2^k 、價值為 v_i 2^k 的若干件物品,其中 k 取遍滿足 w_i 2^k \le W 的非負整數。這是因為不管最優策略選幾件第 i 種物品,總可以表示成若干個剛才這些物品的和(例:13 = 1 + 4 + 8)。這樣就將轉換后的物品數目降成了對數級別。
3. 多重背包3.1 題目
多重背包( )與前面不同就是每種物品是有限個:一共有N種物品,第i(i從1開始)種物品的數量為n[i]完全背包問題算法,重量為w[i],價值為v[i]。在總重量不超過背包承載上限W的情況下,能夠裝入背包的最大價值是多少?
3.2 分析一
此時的分析和完全背包的分析二差不多,也是從裝入第 i 種物品多少件出發:裝入第i種物品0件、1件、...n[i]件(還要滿足不超過限重)。所以狀態方程為:
# k為裝入第i種物品的件數, k <= min(n[i], j/w[i])
dp[i][j] = max{(dp[i-1][j ? k*w[i]] + k*v[i]) for every k}同理也可以進行空間優化,而且 j 也必須逆向枚舉,優化后偽代碼為

// 完全背包問題思路二偽代碼(空間優化版)
dp[0,...,W] = 0
for i = 1,...,N
for j = W,...,w[i] // 必須逆向枚舉!!!
for k = [0, 1,..., min(n[i], j/w[i])]
dp[j] = max(dp[j], dp[j?k*w[i]]+k*v[i])總的時間復雜度約為 O(NW{\bar{n}}) = O(W \sum_i {n_i}) 級別。
3.3 分析二、轉換成01背包
采用2.4節類似的思路可以將多重背包轉換成01背包問題,采用二進制思路將第 i 種物品分成了 O() 件物品,將原問題轉化為了復雜度為 O(W \sum_i{}) 的 01 背包問題,相對于分析一是很大的改進。
4. 其他情形
除了上述三種基本的背包問題外,還有一些其他的變種,如下圖所示(圖片來源)。
本節列舉幾種比較常見的。
4.1 恰好裝滿
背包問題有時候還有一個限制就是必須恰好裝滿背包,此時基本思路沒有區別,只是在初始化的時候有所不同。
如果沒有恰好裝滿背包的限制,我們將dp全部初始化成0就可以了。因為任何容量的背包都有一個合法解“什么都不裝”,這個解的價值為0,所以初始時狀態的值也就全部為0了。如果有恰好裝滿的限制,那只應該將dp[0,...,N][0]初始為0,其它dp值均初始化為-inf,因為此時只有容量為0的背包可以在什么也不裝情況下被“恰好裝滿”,其它容量的背包初始均沒有合法的解,應該被初始化為-inf。
4.2 求方案總數
除了在給定每個物品的價值后求可得到的最大價值外,還有一類問題是問裝滿背包或將背包裝至某一指定容量的方案總數。對于這類問題,需要將狀態轉移方程中的 max 改成 sum ,大體思路是不變的。例如若每件物品均是完全背包中的物品,轉移方程即為
dp[i][j] = sum(dp[i?1][j], dp[i][j?w[i]]) // j >= w[i]4.3 二維背包
前面討論的背包容量都是一個量:重量。二維背包問題是指每個背包有兩個限制條件(比如重量和體積限制),選擇物品必須要滿足這兩個條件。此類問題的解法和一維背包問題不同就是dp數組要多開一維,其他和一維背包完全一樣,例如5.4節。
4.4 求最優方案
一般而言,背包問題是要求一個最優值,如果要求輸出這個最優值的方案,可以參照一般動態規劃問題輸出方案的方法:記錄下每個狀態的最優值是由哪一個策略推出來的,這樣便可根據這條策略找到上一個狀態,從上一個狀態接著向前推即可。
以01背包為例,我們可以再用一個數組G[i][j]來記錄方案,設 G[i][j] = 0表示計算 dp[i][j] 的值時是采用了max中的前一項(也即dp[i?1][j]),G[i][j] = 1 表示采用了方程的后一項。即分別表示了兩種策略: 未裝入第 i 個物品及裝了第 i 個物品。其實我們也可以直接從求好的dp[i][j]反推方案:若 dp[i][j] = dp[i?1][j] 說明未選第i個物品,反之說明選了。
5. 相關題目
本節對上面的背包問題進行討論。
5.1 Equal Sum(分割等和子集)
題目給定一個只包含正整數的非空數組。問是否可以將這個數組分割成兩個子集,使得兩個子集的元素和相等。
由于所有元素的和sum已知,所以兩個子集的和都應該是sum/2(所以前提是sum不能是奇數),即題目轉換成從這個數組里面選取一些元素使這些元素和為sum/2。如果我們將所有元素的值看做是物品的重量,每件物品價值都為1,所以這就是一個恰好裝滿的01背包問題。
我們定義空間優化后的狀態數組dp,由于是恰好裝滿,所以應該將dp[0]初始化為0而將其他全部初始化為,然后按照類似1.2節的偽代碼更新dp:
int capacity = sum / 2;

vector<int>dp(capacity + 1, INT_MIN);
dp[0] = 0;
for(int i = 1; i <= n; i++)
for(int j = capacity; j >= nums[i-1]; j--)
dp[j] = max(dp[j], 1 + dp[j - nums[i-1]]);
更新完畢后,如果dp[sum/2]大于0說明滿足題意。
由于此題最后求的是能不能進行劃分,所以dp的每個元素定義成bool型就可以了,然后將dp[0]初始為true其他初始化為false,而轉移方程就應該是用或操作而不是max操作。完整代碼如下:
bool canPartition(vector<int>& nums) {
int sum = 0, n = nums.size();
for(int &num: nums) sum += num;
if(sum % 2) return false;
int capacity = sum / 2;
vector<bool>dp(capacity + 1, false);
dp[0] = true;
for(int i = 1; i <= n; i++)
for(int j = capacity; j >= nums[i-1]; j--)
dp[j] = dp[j] || dp[j - nums[i-1]];
return dp[capacity];
}
另外此題還有一個更巧妙更快的解法,基本思路是用一個來記錄所有可能子集的和,詳見我的。5.2 Coin (零錢兌換)
題目給定一個價值和一些面值,假設每個面值的硬幣數都是無限的,問我們最少能用幾個硬幣組成給定的價值。
如果我們將面值看作是物品,面值金額看成是物品的重量,每件物品的價值均為1,這樣此題就是是一個恰好裝滿的完全背包問題了。不過這里不是求最多裝入多少物品而是求最少,我們只需要將2.2節的轉態轉移方程中的max改成min即可,又由于是恰好裝滿,所以除了dp[0],其他都應初始化為。完整代碼如下:
int coinChange(vector<int>& coins, int amount) {
vector<int>dp(amount + 1, INT_MAX);
dp[0] = 0;
for(int i = 1; i <= coins.size(); i++)

for(int j = coins[i-1]; j <= amount; j++){
// 下行代碼會在 1+INT_MAX 時溢出
// dp[j] = min(dp[j], 1 + dp[j - coins[i-1]]);
if(dp[j] - 1 > dp[j - coins[i-1]])
dp[j] = 1 + dp[j - coins[i-1]];
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
注意上面1 + dp[j - coins[i-1]]會存在溢出的風險,所以我們換了個寫法。
另外此題還可以進行搜索所有可能然后保持一個全局的結果res,但是直接搜索會超時,所以需要進行精心剪枝,剪枝后可擊敗99%。詳見我的。5.3 Sum(目標和)
這道題給了我們一個數組(元素非負),和一個目標值,要求給數組中每個數字前添加正號或負號所組成的表達式結果與目標值S相等,求有多少種情況。
假設所有元素和為sum,所有添加正號的元素的和為A,所有添加負號的元素和為B,則有sum = A + B 且 S = A - B,解方程得A = (sum + S)/2。即題目轉換成:從數組中選取一些元素使和恰好為(sum + S) / 2。可見這是一個恰好裝滿的01背包問題,要求所有方案數,將1.2節狀態轉移方程中的max改成求和即可。需要注意的是,雖然這里是恰好裝滿,但是dp初始值不應該是inf,因為這里求的不是總價值而是方案數,應該全部初始為0(除了dp[0]初始化為1)。所以代碼如下:
int findTargetSumWays(vector<int>& nums, int S) {
int sum = 0;
// for(int &num: nums) sum += num;
sum = accumulate(nums.begin(), nums.end(), 0);
if(S > sum || sum < -S) return 0; // 肯定不行
if((S + sum) & 1) return 0; // 奇數
int target = (S + sum) >> 1;
vector<int>dp(target + 1, 0);
dp[0] = 1;
for(int i = 1; i <= nums.size(); i++)
for(int j = target; j >= nums[i-1]; j--)
dp[j] = dp[j] + dp[j - nums[i-1]];
return dp[target];
}
5.4 Ones and Zeros(一和零)
題目給定一個僅包含 0 和 1 字符串的數組。任務是從數組中選取盡可能多的字符串,使這些字符串包含的0和1的數目分別不超過m和n。
我們把每個字符串看做是一件物品,把字符串中0的數目和1的數目看做是兩種“重量”,所以就變成了一個二維01背包問題,書包的兩個限重分別是 m 和 n,要求書包能裝下的物品的最大數目(也相當于價值最大,設每個物品價值為1)。
我們可以提前把每個字符串的兩個“重量” w0和w1算出來用數組存放,但是注意到只需要用一次這兩個值,所以我們只需在用到的時候計算w0和w1就行了,這樣就不用額外的數組存放。完整代碼如下:
int findMaxForm(vector<string>& strs, int m, int n) {
int num = strs.size();
int w0, w1;
vector<vector<int>>dp(m+1, vector<int>(n+1, 0));
for(int i = 1; i <= num; i++){
w0 = 0; w1 = 0;
// 計算第i-1個字符串的兩個重量
for(char &c: strs[i - 1]){
if(c == '0') w0 += 1;
else w1 += 1;
}
// 01背包, 逆向迭代更新dp
for(int j = m; j >= w0; j--)
for(int k = n; k >= w1; k--)
dp[j][k] = max(dp[j][k], 1+dp[j-w0][k-w1]);
}
return dp[m][n];
}
6. 總結
本文討論了幾類背包問題及相關題目,其中01背包問題和完全背包問題是最常考的,另外還需要注意一些其他變種例如恰好裝滿、二維背包、求方案總數等等。除了本文討論的這些背包問題之外,還存在一些其他的變種,但只要深刻領會本文所列的背包問題的思路和狀態轉移方程,遇到其它的變形問題,應該也不難想出算法。如果想更加詳細地理解背包問題,推薦閱讀經典的背包問題九講。
參考
更多我的中文題解,可前往查看://