
一、什么是拓?fù)渑判颍?/p>
在圖論中,拓?fù)渑判颍?)是一個(gè)有向無(wú)環(huán)圖(DAG, Graph)的所有頂點(diǎn)的線性序列。且該序列必須滿足下面兩個(gè)條件:
有向無(wú)環(huán)圖(DAG)才有拓?fù)渑判颍荄AG圖沒(méi)有拓?fù)渑判蛞徽f(shuō)。
例如,下面這個(gè)圖:
它是一個(gè) DAG 圖,那么如何寫(xiě)出它的拓?fù)渑判蚰兀窟@里說(shuō)一種比較常用的方法:
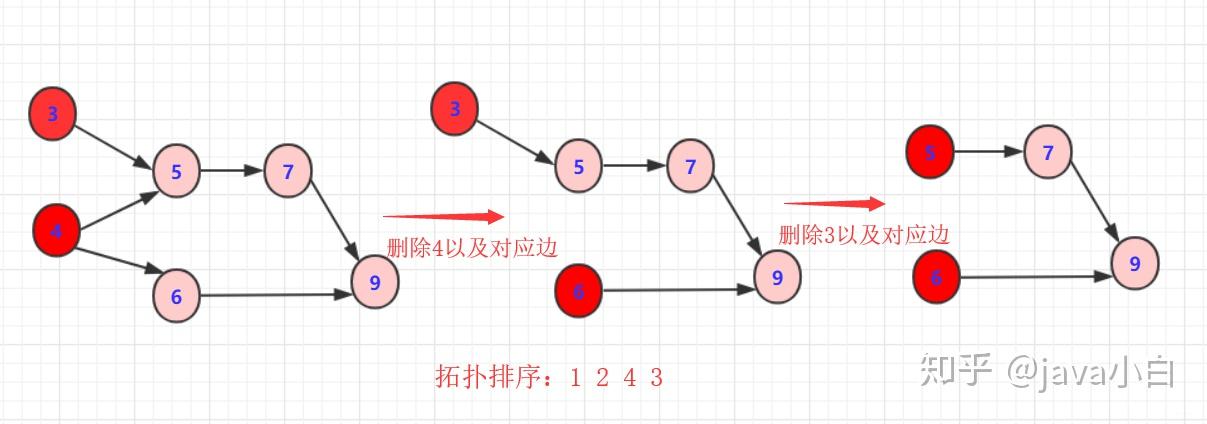
從 DAG 圖中選擇一個(gè)沒(méi)有前驅(qū)(即入度為0)的頂點(diǎn)并輸出。
從圖中刪除該頂點(diǎn)和所有以它為起點(diǎn)的有向邊。
重復(fù) 1 和 2 直到當(dāng)前的 DAG 圖為空或當(dāng)前圖中不存在無(wú)前驅(qū)的頂點(diǎn)為止。
于是,得到拓?fù)渑判蚝蟮慕Y(jié)果是 { 1, 2, 4, 3, 5 }。
通常,一個(gè)有向無(wú)環(huán)圖可以有一個(gè)或多個(gè)拓?fù)渑判蛐蛄小_@是因?yàn)榭赡芡瑫r(shí)存在多個(gè)入度為0的結(jié)點(diǎn),這時(shí),先處理哪個(gè)都是可以的。
二. 拓?fù)渑判蛴脕?lái)干什么?
拓?fù)渑判蛴袃煞N方式拓?fù)渑判蚺袛嗍欠裼协h(huán),就是bfs和dfs,一般書(shū)中介紹的大多數(shù)是bfs,大家就以為拓?fù)渑判蛑挥幸环N辦法,其實(shí)是不對(duì)的。
參考鏈接 :
三、拓?fù)渑判虻腷fs模板
有一個(gè)明確的思路:每一個(gè)頂點(diǎn)都有入度和出度,入度為0說(shuō)明沒(méi)有指向他的,那么就從他開(kāi)始往下找。把這個(gè)入度為0的push進(jìn)隊(duì)列(還要注意保存入度為0的點(diǎn)),同時(shí)把與這個(gè)點(diǎn)相連的所有點(diǎn)的入度-1,然后再看看有沒(méi)有入度為0的,有的話繼續(xù)push,循環(huán)上面的操作,直到?jīng)]有入度為0的點(diǎn)。
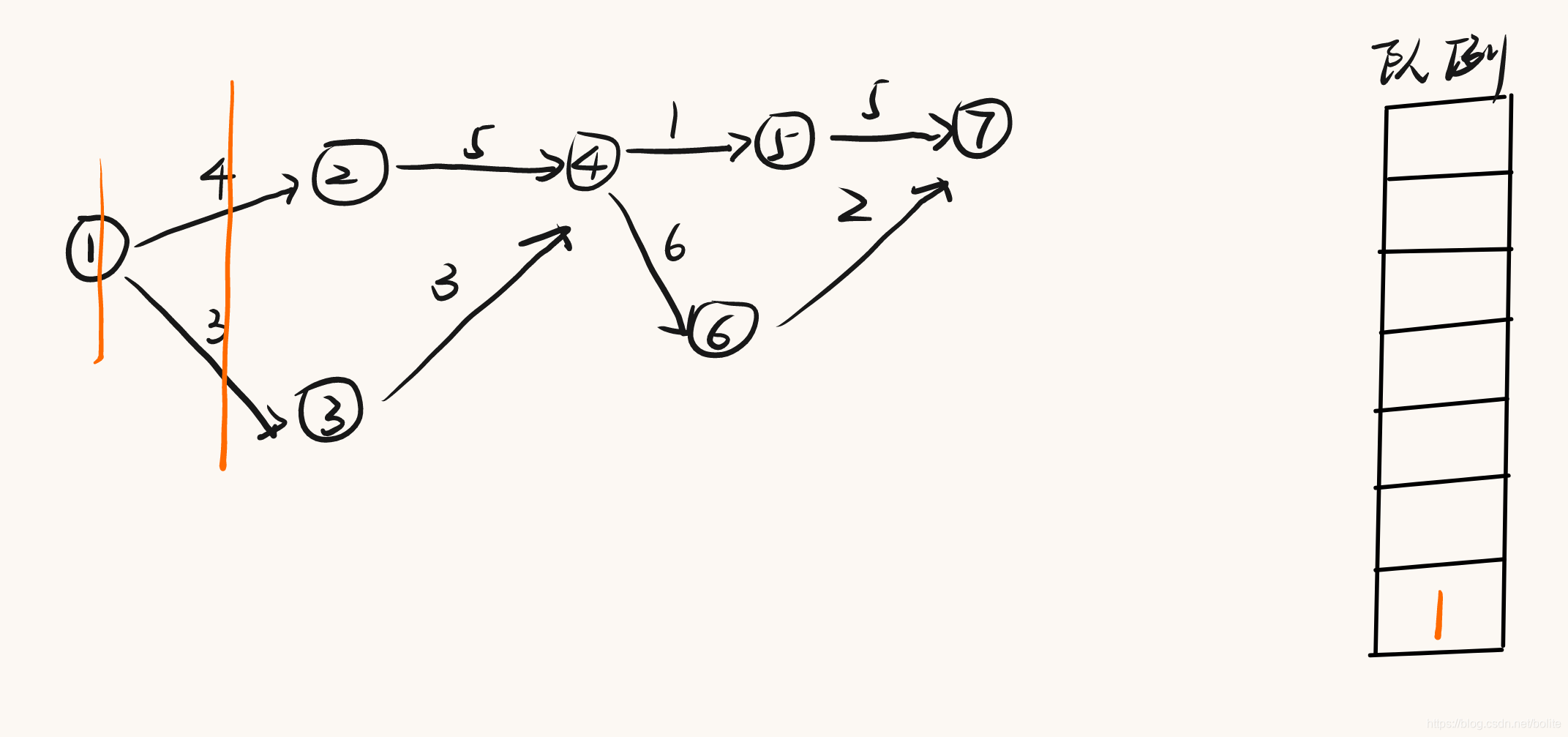
看一下上面的圖,如果從序號(hào)1開(kāi)始的話:1入度為0,push進(jìn)隊(duì)列,頂點(diǎn)2的入度-1,所以頂點(diǎn)2push進(jìn)隊(duì)列,3和5的入度-1,3push進(jìn)隊(duì)列,5push進(jìn)隊(duì)列,頂點(diǎn)3進(jìn)隊(duì)列后,頂點(diǎn)4入度-1,頂點(diǎn)4push進(jìn)隊(duì)列,所以輸出結(jié)果就是1 2 3 5 4
#include
using namespace std;
const int INF = 0x3f3f3f3f;
//本代碼功能:以bfs輸出一個(gè)有向無(wú)環(huán)圖DAG的拓?fù)湫?const int N = 1010;
vector edge[N]; //鄰接表
int ind[N]; //入度數(shù)組
queue q; //隊(duì)列
int n; //n個(gè)結(jié)點(diǎn)
int m; //m條邊
int main() {
//讀入,建圖
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
edge[x].push_back(y);
ind[y]++;//維護(hù)入度
}
//入度為零的放入隊(duì)列
for (int i = 1; i <= n; i++) if (!ind[i]) q.push(i);

//廣度優(yōu)先搜索DAG,就是拓?fù)渑判虻哪0? while (!q.empty()) {
int x = q.front();
q.pop();
//輸出拓?fù)湫? cout << x << " ";
for (int i = 0; i < edge[x].size(); i++) { //遍歷所有出邊
int y = edge[x][i]; //目標(biāo)結(jié)點(diǎn)
//對(duì)接點(diǎn)入度-1,抹去這條入邊
ind[y]--;
//如果入度為0,則入隊(duì)列,準(zhǔn)備處理它
if (!ind[y]) q.push(y);
}
}
return 0;
}
四、拓?fù)渑判虻膁fs模板
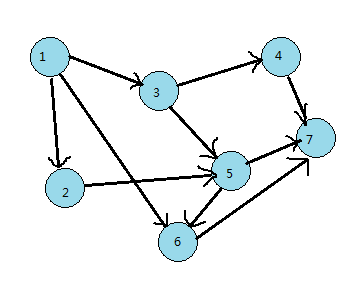
DFS是從一個(gè)點(diǎn)不斷往下遞歸,比如說(shuō)從序號(hào)1往下遞歸,有箭頭就一直往下進(jìn)行,直到到了最后一個(gè)元素拓?fù)渑判蚺袛嗍欠裼协h(huán),就開(kāi)始往棧里(當(dāng)然也可以是之類(lèi)的,只不過(guò)需要反向再輸出)push元素。比如說(shuō)上面的從序號(hào)1開(kāi)始,到序號(hào)2,序號(hào)3,序號(hào)4,到盡頭了,就把4push進(jìn)棧中,3push進(jìn)棧,這個(gè)時(shí)候由于5也是2的下一個(gè)元素,所以5push進(jìn)棧中,2push進(jìn)棧,1push進(jìn)棧,然后輸出就是1 2 5 3 4.

當(dāng)然這個(gè)遞歸的順序是與你輸入的順序有關(guān)的,不過(guò)思路都是這樣的,由起始點(diǎn)向下遞歸。
#include
using namespace std;
const int INF = 0x3f3f3f3f;
//本代碼功能:以dfs輸出一個(gè)有向無(wú)環(huán)圖DAG的拓?fù)湫?const int N = 1010;
bool st[N]; //標(biāo)識(shí)是不是已經(jīng)使用過(guò)
vector edge[N]; //鄰接表
vector res; //拓?fù)湫蛄?/**
* 功能:深度優(yōu)先搜索,記錄拓?fù)湫? * @param u
*/
void dfs(int u) {
//如果訪問(wèn)過(guò)了,則返回,不再重復(fù)訪問(wèn)
if (st[u])return;
//標(biāo)識(shí)u結(jié)點(diǎn)已使用
st[u] = true;
//遍歷每個(gè)出邊,找到下一組結(jié)點(diǎn)
for (int v:edge[u]) if (!st[v]) dfs(v);
//這一層完畢才把它自己扔進(jìn)去,最后扔等于最先輸出,因?yàn)楹竺媸堑剐蜉敵龅? res.push_back(u);
}
int n; //n個(gè)結(jié)點(diǎn)
int m; //m條邊
int main() {
//讀入,建圖
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
edge[x].push_back(y);
}
//將所有結(jié)點(diǎn)進(jìn)行深入優(yōu)先搜索
for (int i = 1; i <= n; i++) dfs(i);
//輸出,從后向前輸出
for (int i = res.size() - 1; i >= 0; i--)
cout << res[i] << " ";
}
測(cè)試數(shù)據(jù):
/**
5 4
1 2
2 3
2 5
3 4
參考答案:
1 2 5 3 4
*/