
神經網絡 算法 思路?能否提供一個最簡單的代碼? 30
。
最基本的BP算法:1)正向傳播:輸入樣本->輸入層->各隱層(處理)->輸出層注1:若輸出層實際輸出與期望輸出(教師信號)不符,則轉入2)(誤差反向傳播過程)2)誤差反向傳播:輸出誤差(某種形式)->隱層(逐層)->輸入層其主要目的是通過將輸出誤差反傳,將誤差分攤給各層所有單元,從而獲得各層單元的誤差信號,進而修正各單元的權值(其過程,是一個權值調整的過程)。
注2:權值調整的過程,也就是網絡的學習訓練過程(學習也就是這么的由來,權值調整)。上傳代碼的第一個案例即是BP的詳細代碼,沒有使用內置函數。
谷歌人工智能寫作項目:小發貓
在搭建神經網絡的時候,如何選擇合適的轉移函數(
一般來說,神經網絡的激勵函數有以下幾種:階躍函數,準線性函數,雙曲正切函數,函數等等,其中函數就是你所說的S型函數rfid。
以我看來,在你訓練神經網絡時,激勵函數是不輕易換的,通常設置為S型函數。如果你的神經網絡訓練效果不好,應從你所選擇的算法上和你的數據上找原因。
算法上BP神經網絡主要有自適應學習速率動量梯度下降反向傳播算法(),-反向傳播算法()等等,我列出的這兩種是最常用的,其中BP默認的是后一種。
數據上,看看是不是有誤差數據,如果有及其剔除,否則也會影響預測或識別的效果。
如何用70行java代碼實現深度神經網絡算法
。
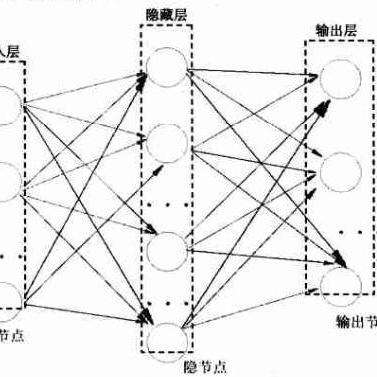
神經網絡結構如下圖所示,最左邊的是輸入層,最右邊的是輸出層,中間是多個隱含層,對于隱含層和輸出層的每個神經節點,都是由上一層節點乘以其權重累加得到,標上“+1”的圓圈為截距項b,對輸入層外每個節點:Y=w0*x0+w1*x1+...+wn*xn+b,由此我們可以知道神經網絡相當于一個多層邏輯回歸的結構。
.;{[][]layer;//神經網絡各層節點[][];//神經網絡各節點誤差[][][];//各層節點權重[][][];//各層節點權重動量;//動量系數;//學習系數(int[],,){=mobp;=rate;layer=[.][];=[.][];=[.][][];=[.][][];=();for(intl=0;l。
如何用70行Java代碼實現神經網絡算法
。
如何用70行Java代碼實現神經網絡算法.;{[][]layer;//神經網絡各層節點[][];//神經網絡各節點誤差[][][];//各層節點權重[][][];//各層節點權重動量;//動量系數;//學習系數(int[],,){=mobp;=rate;layer=[.][];=[.][];=[.][][];=[.][][];=();for(intl=0;l。
神經網絡模型
你自行搭建的神經網絡模型,權值和閾值仍然是要通過訓練得到的。初始化后,將BP算法加到這個模型上,不斷調整權值。可以先用神經網絡工具箱訓練好一個網絡,再將權值和閾值導出。
{1,1}=W1;{2,1}=W2;net.b{1}=B1;net.b{2}=B2;注意要反過來,如果是導出的話。
如何用70行Java代碼實現深度神經網絡算法
。
參考下面代碼:.;{[][]layer;//神經網絡各層節點[][];//神經網絡各節點誤差[][][];//各層節點權重[][][];//各層節點權重動量;//動量系數;//學習系數(int[],,){=mobp;=rate;layer=[.][];=[.][];=[.][][];=[.][][];=();for(intl=0;l。
傷寒、副傷寒流行預測模型(BP神經網絡)的建立
由于目前研究的各種數學模型或多或少存在使用條件的局限性,或使用方法的復雜性等問題,預測效果均不十分理想,距離實際應用仍有較大差距。
NNT是中較為重要的一個工具箱,在實際應用中,BP網絡用的最廣泛。
神經網絡具有綜合能力強,對數據的要求不高,適時學習等突出優點,其操作簡便,節省時間,網絡初學者即使不了解其算法的本質,也可以直接應用功能豐富的函數來實現自己的目的。
因此,易于被基層單位預防工作者掌握和應用。
以下幾個問題是建立理想的因素與疾病之間的神經網絡模型的關鍵:(1)資料選取應盡可能地選取所研究地區系統連續的因素與疾病資料,最好包括有疾病高發年和疾病低發年的數據。
在收集影響因素時,要抓住主要影響傷寒、副傷寒的發病因素。
(2)疾病發病率分級神經網絡預測法是按發病率高低來進行預測,在定義發病率等級時,要結合專業知識及當地情況而定,并根據網絡學習訓練效果而適時調整,以使網絡學習訓練達到最佳效果。
(3)資料處理問題在實踐中發現,資料的特征往往很大程度地影響網絡學習和訓練的穩定性,因此,數據的應用、納入、排出問題有待于進一步研究。
6.3.1人工神經網絡的基本原理人工神經網絡(ANN)是近年來發展起來的十分熱門的交叉學科,它涉及生物、電子、計算機、數學和物理等學科,有著廣泛的應用領域。
人工神經網絡是一種自適應的高度非線性動力系統,在網絡計算的基礎上,經過多次重復組合,能夠完成多維空間的映射任務。
神經網絡通過內部連接的自組織結構,具有對數據的高度自適應能力,由計算機直接從實例中學習獲取知識,探求解決問題的方法,自動建立起復雜系統的控制規律及其認知模型。
人工神經網絡就其結構而言,一般包括輸入層、隱含層和輸出層,不同的神經網絡可以有不同的隱含層數,但他們都只有一層輸入和一層輸出。
神經網絡的各層又由不同數目的神經元組成,各層神經元數目隨解決問題的不同而有不同的神經元個數。
6.3.2BP神經網絡模型BP網絡是在1985年由PDP小組提出的反向傳播算法的基礎上發展起來的,是一種多層次反饋型網絡(圖6.17),它在輸入和輸出之間采用多層映射方式,網絡按層排列,只有相鄰層的節點直接相互連接,傳遞之間信息。
在正向傳播中,輸入信息從輸入層經隱含層逐層處理,并傳向輸出層,每層神經元的狀態只影響下一層神經元的狀態。
如果輸出層不能得到期望的輸出結果,則轉入反向傳播,將誤差信號沿原來的連同通路返回,通過修改各層神經元的權值,使誤差信號最小。
BP網絡的學習算法步驟如下(圖6.18):圖6.17BP神經網絡示意圖圖6.18BP算法流程圖第一步:設置初始參數ω和θ,(ω為初始權重,θ為臨界值,均隨機設為較小的數)。
第二步:將已知的樣本加到網絡上,利用下式可算出他們的輸出值yi,其值為巖溶地區地下水與環境的特殊性研究式中:xi為該節點的輸入;ωij為從I到j的聯接權;θj為臨界值;yj為實際算出的輸出數據。
第三步:將已知輸出數據與上面算出的輸出數據之差(dj-yj)調整權系數ω,調整量為ΔWij=ηδjxj式中:η為比例系數;xj為在隱節點為網絡輸入,在輸出點則為下層(隱)節點的輸出(j=1,2…,n);dj為已知的輸出數據(學習樣本訓練數據);δj為一個與輸出偏差相關的值,對于輸出節點來說有δj=ηj(1-yj)(dj-yj)對于隱節點來說,由于它的輸出無法進行比較,所以經過反向逐層計算有巖溶地區地下水與環境的特殊性研究其中k指要把上層(輸出層)節點取遍。
誤差δj是從輸出層反向逐層計算的。各神經元的權值調整后為ωij(t)=ωij(t-1)+Vωij式中:t為學習次數。
這個算法是一個迭代過程,每一輪將各W值調整一遍,這樣一直迭代下去,知道輸出誤差小于某一允許值為止,這樣一個好的網絡就訓練成功了,BP算法從本質上講是把一組樣本的輸入輸出問題變為一個非線性優化問題,它使用了優化技術中最普遍的一種梯度下降算法,用迭代運算求解權值相當于學習記憶問題。

6.3.3BP神經網絡模型在傷寒、副傷寒流行與傳播預測中的應用傷寒、副傷寒的傳播與流行同環境之間有著一定的聯系。
根據桂林市1990年以來鄉鎮為單位的傷寒、副傷寒疫情資料,傷寒、副傷寒疫源地資料,結合現有資源與環境背景資料(桂林市行政區劃、土壤、氣候等)和社會經濟資料(經濟、人口、生活習慣等統計資料)建立人工神經網絡數學模型,來逼近這種規律。
6.3.3.1模型建立(1)神經網絡的BP算法BP網絡是一種前饋型網絡,由1個輸入層、若干隱含層和1個輸出層構成。
如果輸入層、隱含層和輸出層的單元個數分別為n,q1,q2,m,則該三層網絡網絡可表示為BP(n,q1,q2,m),利用該網絡可實現n維輸入向量Xn=(X1,X2,…,Xn)T到m維輸出向量Ym=(Y1,Y2,…,Ym)T的非線性映射。
輸入層和輸出層的單元數n,m根據具體問題確定。
(2)樣本的選取將模型的輸入變量設計為平均溫度、平均降雨量、巖石性質、巖溶發育、地下水類型、飲用水類型、正規自來水供應比例、集中供水比例8個輸入因子(表6.29),輸出單元為傷寒副傷寒的發病率等級,共一個輸出單元。
其中q1,q2的值根據訓練結果進行選擇。表6.29桂林市傷寒副傷寒影響因素量化表通過分析,選取在傷寒副傷寒有代表性的縣鎮在1994~2001年的環境參評因子作為樣本進行訓練。
利用聚類分析法對疫情進行聚類分級(Ⅰ、Ⅱ、Ⅲ、Ⅳ),傷寒副傷寒發病最高級為Ⅳ(BP網絡中輸出定為4),次之的為Ⅲ(BP網絡中輸出定為3),以此類推,最低為Ⅰ(BP網絡中輸出定為1)(3)數據的歸一化處理為使網絡在訓練過程中易于收斂,我們對輸入數據進行了歸一化處理,并將輸入的原始數據都化為0~1之間的數。
如將平均降雨量的數據乘以0.0001;將平均氣溫的數據乘以0.01;其他輸入數據也按類似的方法進行歸一化處理。
(4)模型的算法過程假設共有P個訓練樣本,輸入的第p個(p=1,2,…,P)訓練樣本信息首先向前傳播到隱含單元上。
經過激活函數f(u)的作用得到隱含層1的輸出信息:巖溶地區地下水與環境的特殊性研究經過激活函數f(u)的作用得到隱含層2的輸出信息:巖溶地區地下水與環境的特殊性研究激活函數f(u)我們這里采用型,即f(u)=1/[1+exp(-u)](6.5)隱含層的輸出信息傳到輸出層,可得到最終輸出結果為巖溶地區地下水與環境的特殊性研究以上過程為網絡學習的信息正向傳播過程。
另一個過程為誤差反向傳播過程。
如果網絡輸出與期望輸出間存在誤差,則將誤差反向傳播,利用下式來調節網絡權重和閾值:巖溶地區地下水與環境的特殊性研究式中:Δω(t)為t次訓練時權重和閾值的修正;η稱為學習速率,0<η<1;E為誤差平方和。
巖溶地區地下水與環境的特殊性研究反復運用以上兩個過程,直至網絡輸出與期望輸出間的誤差滿足一定的要求。該模型算法的缺點:1)需要較長的訓練時間。
由于一些復雜的問題,BP算法可能要進行幾小時甚至更長的時間的訓練,這主要是由于學習速率太小造成的,可采用變化的學習速率或自適應的學習速率加以改進。2)完全不能訓練。

主要表現在網絡出現的麻痹現象上,在網絡的訓練過程中,當其權值調的過大,可能使得所有的或大部分神經元的加權總和n偏大,這使得激活函數的輸入工作在S型轉移函數的飽和區,從而導致其導數f′(n)非常小,從而使得對網絡權值的調節過程幾乎停頓下來。
3)局部極小值。BP算法可以使網絡權值收斂到一個解,但它并不能保證所求為誤差超平面的全局最小解,很可能是一個局部極小解。
這是因為BP算法采用的是梯度下降法,訓練從某一起點沿誤差函數的斜面逐漸達到誤差的最小值。
考慮到以上算法的缺點,對模型進行了兩方面的改進:(1)附加動量法為了避免陷入局部極小值,對模型進行了改進多層神經網絡bp算法權值更新過程,應用了附加動量法。
附加動量法在使網絡修正及其權值時,不僅考慮誤差在梯度上的作用,而且考慮在誤差曲面上變化趨勢的影響,其作用如同一個低通濾波器,它允許網絡忽略網絡上的微小變化特性。
在沒有附加動量的作用下,網絡可能陷入淺的局部極小值,利用附加動量的作用則有可能滑過這些極小值。
該方法是在反向傳播法的基礎上在每一個權值的變化上加上一項正比于前次權值變化量的值多層神經網絡bp算法權值更新過程,并根據反向傳播法來產生心的權值變化。
促使權值的調節向著誤差曲面底部的平均方向變化,從而防止了如Δω(t)=0的出現,有助于使網絡從誤差曲面的局部極小值中跳出。
這種方法主要是把式(6.7)改進為巖溶地區地下水與環境的特殊性研究式中:A為訓練次數;a為動量因子,一般取0.95左右。
訓練中對采用動量法的判斷條件為巖溶地區地下水與環境的特殊性研究(2)自適應學習速率對于一個特定的問題,要選擇適當的學習速率不是一件容易的事情。
通常是憑經驗或實驗獲取,但即使這樣,對訓練開始初期功效較好的學習速率,不見得對后來的訓練合適。
所以,為了盡量縮短網絡所需的訓練時間,采用了學習速率隨著訓練變化的方法來找到相對于每一時刻來說較差的學習速率。
下式給出了一種自適應學習速率的調整公式:巖溶地區地下水與環境的特殊性研究通過以上兩個方面的改進,訓練了一個比較理想的網絡,將動量法和自適應學習速率結合起來,效果要比單獨使用要好得多。
6.3.3.2模型的求解與預測采用包含了2個隱含層的神經網絡BP(4,q1,q2,1),隱含層單元數q1,q2與所研究的具體問題有關,目前尚無統一的確定方法,通常根據網絡訓練情況采用試錯法確定。
在滿足一定的精度要求下一般認小的數值,以改善網絡的概括推論能力。
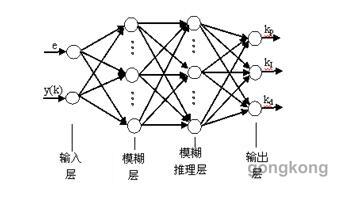
在訓練中網絡的收斂采用輸出值Ykp與實測值tp的誤差平方和進行控制:巖溶地區地下水與環境的特殊性研究1)將附加動量法和自適應學習速率結合應用,分析桂林市36個鄉鎮地質條件各因素對傷寒副傷寒發病等級的影響。
因此訓練樣本為36個,第一個隱含層有19個神經元,第二個隱含層有11個神經元,學習速率為0.001。A.程序(略)。B.網絡訓練。
在命令窗口執行運行命令,網絡開始學習和訓練,其學習和訓練過程如下(圖6.19)。圖6.19神經網絡訓練過程圖C.模型預測。
a.輸入未參與訓練的鄉鎮(洞井鄉、兩水鄉、延東鄉、四塘鄉、嚴關鎮、靈田鄉)地質條件數據。b.預測。程序運行后網絡輸出預測值a3,與已知的實際值進行比較,其預測結果整理后見(表6.30)。
經計算,對6個鄉鎮傷寒副傷寒發病等級的預測符合率為83.3%。表6.30神經網絡模型預測結果與實際結果比較c.地質條件改進方案。
在影響疾病發生的地質條件中,大部分地質條件是不會變化的,而改變發病地區的飲用水類型是可以人為地通過改良措施加以實施的一個因素。
因此,以靈田鄉為例對發病率較高的鄉鎮進行分析,改變其飲用水類型,來看發病等級的變化情況。
表6.31顯示,在其他地質條件因素不變的情況下,改變當地的地下水類型(從原來的巖溶水類型改變成基巖裂隙水)則將發病等級從原來的最高級4級,下降為較低的2級,效果是十分明顯的。
因此,今后在進行傷寒副傷寒疾病防治的時候,可以通過改變高發區飲用水類型來客觀上減少疫情的發生。
表6.31靈田鄉改變飲用水類型前后的預測結果2)選取桂林地區1994~2000年月平均降雨量、月平均溫度作為輸入數據矩陣,進行樣本訓練,設定不同的隱含層單元數,對各月份的數據進行BP網絡訓練。
在隱含層單元數q1=13,q2=9,經過46383次數的訓練,誤差達到精度要求,學習速率0.02。A.附加動量法程序(略)。B.網絡訓練。
在命令窗口執行運行命令,網絡開始學習和訓練,其學習和訓練過程如下(圖6.20)。C.模型預測。a.輸入桂林市2001年1~12月桂林市各月份的平均氣溫和平均降雨量。預測程度(略)。b.預測。
程序運行后網絡輸出預測值a2,與已知的實際值進行比較,其預測結果整理后見(表6.32)。經計算,對2001年1~12月傷寒副傷寒發病等級進行預測,12個預測結果中,有9個符合,符合率為75%。
圖6.20神經網絡訓練過程圖表6.32神經網絡模型預測結果與實際值比較6.3.3.3模型的評價本研究采用BP神經網絡對傷寒、副傷寒發病率等級進行定量預測,一方面引用數量化理論對不確定因素進行量化處理;另一方面利用神經網絡優點,充分考慮各影響因素與發病率之間的非線性映射。
實際應用表明,神經網絡定量預測傷寒、副傷寒發病率是理想的。其主要優點有:1)避免了模糊或不確定因素的分析工作和具體數學模型的建立工作。2)完成了輸入和輸出之間復雜的非線性映射關系。
3)采用自適應的信息處理方式,有效減少人為的主觀臆斷性。雖然如此,但仍存在以下缺點:1)學習算法的收斂速度慢,通常需要上千次或更多,訓練時間長。2)從數學上看,BP算法有可能存在局部極小問題。
本模型具有廣泛的應用范圍,可以應用在很多領域。從上面的結果可以看出,實際和網絡學習數據總體較為接近,演化趨勢也基本一致。
說明選定的氣象因子、地質條件因素為神經單元獲得的傷寒、副傷寒發病等級與實際等級比較接近,從而證明傷寒、副傷寒流行與地理因素的確存在較密切的相關性。