
其實根本就談不上詳解,應該說只是隨便談談,真正能詳解動態規劃的又有幾個人,所以,這個標題略顯扯淡。
前段時間一直在做關于數據結構的題,也算是對數據結構有了一定的了解,知道了有些數據結構的基本算法。現在剛剛開始接觸動態規劃,其實寫這篇文章的初衷是一來鍛煉一下自己的總結能力,二來也是希望通過這篇文章,來指引和我一樣的初學者,廢話不多說了,開始吧。
一、01背包
我最開始接觸的有關動態規劃的是01背包,這應該也是動態規劃入門最好的了吧。 01背包是很簡單的問題,當然也不乏一些變種讓你絞盡腦汁也想不到,這里我們不討論那些,我只說最簡單的。
假設有n種物品,每種都只有一個,第i種物品的體積為Vi,重量為Wi,選一些物品到一個容量為C的背包,使得背包內總物品的體積不超過C的情況下重量最大。
因為每種東西只有放入背包和不放入兩種狀態,這也就是01的由來了。對于這個問題,你當然可以枚舉所有的可能性,如果有n個物品的話,總共有2^n種可能性,如果數據大的話,普通計算機是不可能計算的,當然你可以借一臺超級計算機,這是另外一種情況,不予討論。

我們可以換一種思考方法,對與第i件物品,我們比較把它放入和不放入背包中的重量比較,取最大值,這樣我們就可以得到這樣一個表達式 dp(V) = max(dp(V), dp(V-vi) + wi), 具體實現我們可以采用遞歸的方式。這樣時間復雜度好會不會好很多,很明顯不會,因為會重復計算好多次,舉個簡單例子,如果我們計算dp(6),在這個過程中我們用到了dp(3),而在計算dp(5)的過程中也用到了dp(3),這樣這兩個過程就會重復計算一次dp(3),想想數據量大的話該有多少重復啊。。
關于這個重復計算的問題,我們只要在過程中記錄這些結果就完全可以避免重復計算,還是上面的例子,我們在dp(6)中計算了dp(3),并且將dp(3)的結果保存了,在dp(5)中我們直接調用dp(3),就行了,這種方法被稱為記憶化搜索,因為dp()這個函數你在一定程度上可以把它當做dfs()。
雖然記憶話搜索就是動態規劃的思想,不過這還不是最好的方法完全背包問題算法,我們完全可以把遞歸改成遞推的方式,這樣dp[V] = max(dp[V], dp[V-vi] + wi),這個表達式也被稱為狀態轉移方程,這也是動態規劃的核心,還有,一定要理解01背包這個方程,因為絕大多數狀態轉移方程是由它演變來的。
我們不難寫出遞推的代碼

for (int i = 1; i <= n; i++)
{
for (int j = C; j >= v[i]; j--)
{
dp[i][j] = max(dp[i][j], dp[i-1][j-v[i]] + w[i]);
}
}
時間復雜度為O(n*n),時間上我們沒辦法在優化了,但在空間上我們可以繼續優化,我們可以把dp數組改成一維的,得到以下代碼也是正確的,因為在求解的過會覆蓋掉一部分,但覆蓋之后的值卻是該狀態的最優解。
for (int i = 1; i <= n; i++)
{
for (int j = C; j >= v[i]; j--)
{
dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
}
}
二、最長非降子序列
這個也比較簡單,也是基本的東西,不過越基本的越應該熟悉。
我們讓dp[i] 保存前i個數的最長非降子序列長度,每次計算以第i個數結尾的最長子序列的長度。狀態轉移方程就是dp[i] = max(dp[i],dp[j] + 1)。
#include
#include
int a[100];
int dp[100];
int max(int a, int b)
{
return a > b ?a : b;
}
int main()
{
int n;
scanf("%d",&n);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
for (int i = 1; i <= n; i++)
{
for (int j = 0; j < i; j++)
{
if (a[i] > a[j])
dp[i] = max(dp[i],dp[j] + 1);
}
}
printf("%d\n",dp[n]);
}
三、最長公共子序列(LCS)
動態規劃就是求最優子問題,通過局部最優值來推導全局最優。
先說一下什么是最長公共子序列完全背包問題算法, 比如BDCAB 和 ABCBA兩個字符串,他們的最長公共子序列是 BCBA,長度為4。這里要注意區分字串和子序列,字串要求連續,而子序列不要求連續。
接下來說一下解法
求解最長公共子序列肯定是求解全局最優的問題,可以通過逐步推到求出。 這里我們需要定義一個數組dp[i][j], 數組中的結果表示 第一個字符串從1-i位置 和 第二個字符串從 1-j位置最長公共子序列(需注意這里字符串下標是從1開始的)。

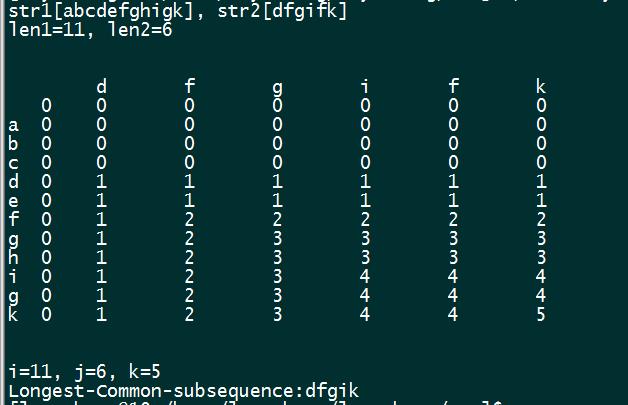
注意看以下這張圖,這是理解LCS 問題的關鍵,途中每個格子里的值表示到這個下標對于字符串最長公共子序列的長度。 我們可以通過dp[i-1][j], dp[i-1][j-1], dp[i][j-1], 這三個格子來推導dp[i][j], 具體方法是, 如果兩個字符串中對應的 i 和j位置(s[i] 和 t[j],圖中豎著為s 橫為t)相同, 那么dp[i][j] = dp[i-1][j-1]+1,因為比 i-1 j-1 對應的字符串多了一個相同的字符, 如果不同,dp[i][j] = max(dp[i-1][j], dp[i][j-1]), 在圖中就是dp[i][j] 左邊和上邊的格子。
圖中每個格子都有一個箭頭,表示的是格子中的值是通過哪個格子計算出來的。
用dp數組只能計算出兩個字符串最長公共子序列的長度,并不能求出這個公共子序列。當然這也是可以求出的,再來看這圖, 灰色的格子中斜著的箭頭所在格子對應的字符按順序組合就是他們最長公共子序列,當然這不是巧合, 我們只需要額外開一個數組來記錄這個箭頭就可以了。不是什么難事。
以下是代碼:
int LCS(char* s, char* t)
{
int dp[MAX][MAX];
int n = strlen(s);
int m = strlen(t);
memset(dp, 0, sizeof(dp));
for(int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (s[i-i] == t[j-1]) //計算的時候下標要從1開始,這里做一下相應的轉換
dp[i][j] = dp[i-1][j-1]+1;
else
dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
return dp[n][m];
}
此文章將持續更新。。。。。。