
? 原創 ·作者|海晨威
學校|同濟大學碩士生
研究方向|自然語言處理
在當前的 NLP 領域, / BERT 已然成為基礎應用,而 Self- 則是兩者的核心部分,下面嘗試用 Q&A 和源碼的形式深入 Self- 的細節。
Q&A
1. Self- 的核心是什么?

Self- 的核心是用文本中的其它詞來增強目標詞的語義表示,從而更好的利用上下文的信息。
2. Self- 的時間復雜度是怎么計算的?
Self- 時間復雜度:,這里,n 是序列的長度,d 是 的維度,不考慮 batch 維。Self- 包括三個步驟:相似度計算, 和加權平均。
它們分別的時間復雜度是:
相似度計算 可以看作大小為 和 的兩個矩陣相乘:,得到一個 的矩陣。 就是直接計算了,時間復雜度為 。加權平均 可以看作大小為 和 的兩個矩陣相乘:,得到一個 的矩陣。因此,Self- 的時間復雜度是 。
這里再提一下 中的 Multi-Head ,多頭 ,簡單來說就是多個 Self- 的組合,它的作用類似于 CNN 中的多核。
多頭的實現不是循環的計算每個頭,而是通過 and ,用矩陣乘法來完成的。
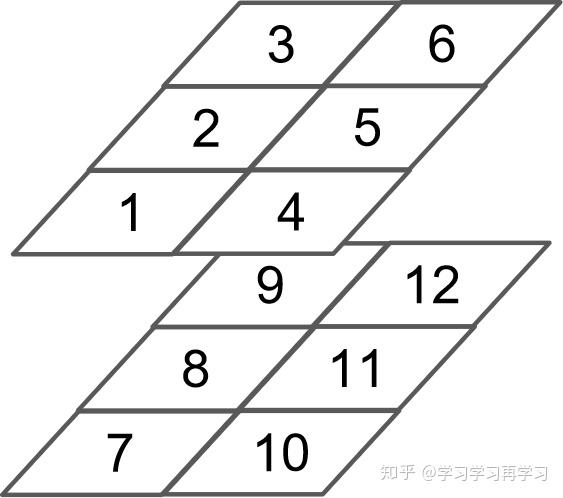
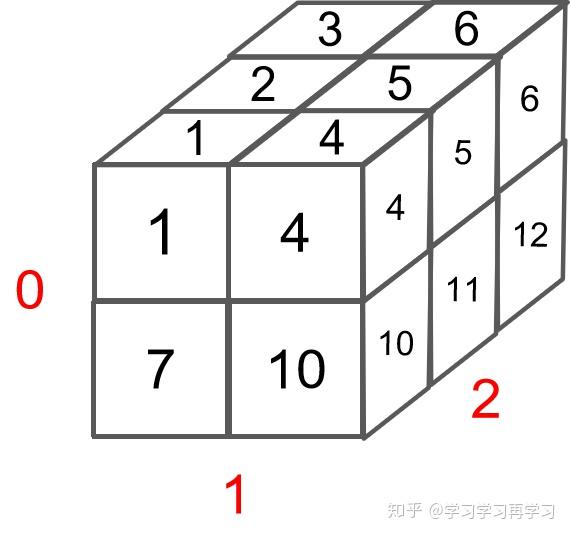
In , the multi- are done with and than . —— 來自 BERT 源代碼注釋/BERT 中把 d ,也就是 / 這個維度做了 拆分,可以去看 的 TF 源碼或者上面的 源碼: (d) = (m) * (a),也即 d=m*a。并將 維度 到前面,使得 Q 和 K 的維度都是 (m,n,a),這里不考慮 batch 維度。這樣點積可以看作大小為 (m,n,a) 和 (m,a,n) 的兩個張量相乘,得到一個 (m,n,n) 的矩陣,其實就相當于 m 個頭,時間復雜度是 。
張量乘法時間復雜度分析參見:矩陣、張量乘法的時間復雜度分析 [1]。
因此 Multi-Head 時間復雜度就是 ,而實際上,張量乘法可以加速,因此實際復雜度會更低一些。
3. 不考慮多頭的原因,self-中詞向量不乘QKV參數矩陣源程序量 是什么,會怎么樣?
對于 機制,都可以用統一的 query/key/value 模式去解釋,而對于 self-,一般會說它的 q=k=v,這里的相等實際上是指它們來自同一個基礎向量,而在實際計算時,它們是不一樣的,因為這三者都是乘了 QKV 參數矩陣的。那如果不乘,每個詞對應的 q,k,v 就是完全一樣的。
在 self- 中, 中的每個詞都會和 中的每個詞做點積去計算相似度,也包括這個詞本身。
在相同量級的情況下,qi 與 ki 點積的值會是最大的(可以從“兩數和相同的情況下,兩數相等對應的積最大”類比過來)。
那在 后的加權平均中源程序量 是什么,該詞本身所占的比重將會是最大的,使得其他詞的比重很少,無法有效利用上下文信息來增強當前詞的語義表示。

而乘以 QKV 參數矩陣,會使得每個詞的 q,k,v 都不一樣,能很大程度上減輕上述的影響。
當然,QKV 參數矩陣也使得多頭,類似于 CNN 中的多核,去捕捉更豐富的特征/信息成為可能。
4. 在常規 中,一般有 k=v,那 self- 可以嘛?
self- 實際只是 中的一種特殊情況,因此 k=v 是沒有問題的,也即 K,V 參數矩陣相同。
擴展到 Multi-Head 中,乘以 Q、K 參數矩陣之后,其實就已經保證了多頭之間的差異性了,在 q 和 k 點積 + 得到相似度之后,從常規 的角度,覺得再去乘以和 k 相等的 v 會更合理一些。
在 / BERT 中,完全獨立的 QKV 參數矩陣,可以擴大模型的容量和表達能力。
但采用 Q,K=V 這樣的參數模式,我認為也是沒有問題的,也能減少模型的參數,又不影響多頭的實現。
當然,上述想法并沒有做過實驗,為個人觀點,僅供參考。
源碼
在整個 / BERT 的代碼中,(Multi-Head Dot-) Self- 的部分是相對最復雜的,也是 / BERT 的精髓所在,這里給出 版本的實現 [2],并對重要的代碼加上了注釋和維度說明。
話不多說,都在代碼里,它主要有三個部分:
初始化:包括有幾個頭,每個頭的大小,并初始化 QKV 三個參數矩陣。
class?SelfAttention(nn.Module):
????def?__init__(self,?config):
????????super(SelfAttention,?self).__init__()
????????if?config.hidden_size?%?config.num_attention_heads?!=?0:
????????????raise?ValueError(
????????????????"The?hidden?size?(%d)?is?not?a?multiple?of?the?number?of?attention?"
????????????????"heads?(%d)"?%?(config.hidden_size,?config.num_attention_heads))
????????#?在Transformer/BERT中,這里的?all_head_size?就等于?config.hidden_size
????????#?應該是一種簡化,為了從embedding到最后輸出維度都保持一致
????????#?這樣使得多個attention頭合起來維度還是config.hidden_size
????????#?而?attention_head_size?就是每個attention頭的維度,要保證可以整除
????????self.num_attention_heads?=?config.num_attention_heads
????????self.attention_head_size?=?int(config.hidden_size?/?config.num_attention_heads)
????????self.all_head_size?=?self.num_attention_heads?*?self.attention_head_size
????????#?三個參數矩陣
????????self.query?=?nn.Linear(config.hidden_size,?self.all_head_size)
????????self.key?=?nn.Linear(config.hidden_size,?self.all_head_size)
????????self.value?=?nn.Linear(config.hidden_size,?self.all_head_size)
????????self.dropout?=?nn.Dropout(config.attention_probs_dropout_prob)
and :這個函數主要是把維度大小為 [ * * ] 的 q,k,v 向量變換成 [ * * * ],便于后面做 Multi-Head 。
????def?transpose_for_scores(self,?x):
????????"""
????????shape?of?x:?batch_size?*?seq_length?*?hidden_size
????????這個操作是把hidden_size分解為?self.num_attention_heads?*?self.attention_head_size
????????然后再交換?seq_length?維度?和?num_attention_heads?維度
????????為什么要做這一步:因為attention是要對query中的每個字和key中的每個字做點積,即是在 seq_length 維度上
????????query和key的點積是?[seq_length?*?attention_head_size]?*?[attention_head_size?*?seq_length]=[seq_length?*?seq_length]
????????"""
????????#?這里是一個維度拼接:(1,2)+(3,4)?->?(1, 2, 3, 4)
????????new_x_shape?=?x.size()[:-1]?+?(self.num_attention_heads,?self.attention_head_size)
????????x?=?x.view(*new_x_shape)
????????return?x.permute(0,?2,?1,?3)
前向計算: 乘以 QKV 參數矩陣 —> and —> 做 —> 加 mask —> —> 加權平均 —> 維度恢復。
?def?forward(self,?hidden_states,?attention_mask):
????????#?shape?of?hidden_states?and?mixed_*_layer:?batch_size?*?seq_length?*?hidden_size
????????mixed_query_layer?=?self.query(hidden_states)
????????mixed_key_layer?=?self.key(hidden_states)
????????mixed_value_layer?=?self.value(hidden_states)
????????#?shape?of?*_layer:?batch_size?*?num_attention_heads?*?seq_length?*?attention_head_size
????????query_layer?=?self.transpose_for_scores(mixed_query_layer)
????????key_layer?=?self.transpose_for_scores(mixed_key_layer)
????????value_layer?=?self.transpose_for_scores(mixed_value_layer)
????????#?Take?the?dot?product?between?"query"?and?"key"?to?get?the?raw?attention?scores.
????????#?shape?of?attention_scores:?batch_size?*?num_attention_heads?*?seq_length?*?seq_length
????????attention_scores?=?torch.matmul(query_layer,?key_layer.transpose(-1,?-2))
????????#?這里就是做?Scaled,將方差統一到1,避免維度的影響
????????attention_scores?/=?math.sqrt(self.attention_head_size)
????????#?shape?of?attention_mask:?batch_size?*?1?*?1?*?seq_length.?它可以自動廣播到和attention_scores一樣的維度
????????#?我們初始輸入的attention_mask是:batch_size * seq_length,做了兩次unsqueeze之后得到當前的attention_mask
????????attention_scores?=?attention_scores?+?attention_mask
????????#?Normalize?the?attention?scores?to?probabilities.?Softmax?不改變維度
????????#?shape?of?attention_scores:?batch_size?*?num_attention_heads?*?seq_length?*?seq_length
????????attention_probs?=?nn.Softmax(dim=-1)(attention_scores)
????????attention_probs?=?self.dropout(attention_probs)
????????#?shape?of?value_layer:?batch_size?*?num_attention_heads?*?seq_length?*?attention_head_size
????????#?shape?of?first?context_layer:?batch_size?*?num_attention_heads?*?seq_length?*?attention_head_size
????????#?shape?of?second?context_layer:?batch_size?*?seq_length?*?num_attention_heads?*?attention_head_size
????????# context_layer 維度恢復到:batch_size * seq_length * hidden_size
????????context_layer?=?torch.matmul(attention_probs,?value_layer)
????????context_layer?=?context_layer.permute(0,?2,?1,?3).contiguous()
????????new_context_layer_shape?=?context_layer.size()[:-2]?+?(self.all_head_size,)
????????context_layer?=?context_layer.view(*new_context_layer_shape)
????????return?context_layer
is all you need ! 希望這篇文章能讓你對 Self- 有更深的理解。
參考文獻
[1]
[2]