
貪心算法貪心算法基本思路
image.png
貪心算法的基本思想
?貪心算法的特點是每個階段所作的選擇都是局部最優的貪心算法部分背包問題,它期望通過所作的局部最優選擇產生出一個全局最優解。
貪心與動態規劃:與動態規劃不同的是,貪心是鼠目寸光;動態規劃是統攬全局。
–動態規劃:每個階段產生的都是全局最優解
?第i階段的“全局”: 問題空間為(a1, … , ai)
?第i階段的“全局最優解”:問題空間為 (a1, … , ai)時的最優解
–貪心:每個階段產生的都是局部最優解
?第i階段的“局部”:問題空間為按照貪心策略中的優先級排好序的第i個輸入ai
?第i階段的“局部最優解”: ai
貪心算法的基本要素
?貪心選擇性質:所求問題的全局最優解可以通過一系列局部最優的選擇(即貪心選擇)來達到。
–這是貪心算法與動態規劃算法的主要區別。
?最優子結構性質:當原問題的最優解包含子問題的最優解時貪心算法部分背包問題,稱此問題具有最優子結構性質。
最優子結構性質是該問題可用動態規劃算法或貪心算法求解的關鍵特征
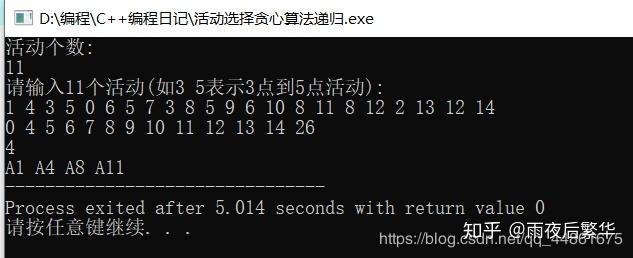
0-1背包——貪心算法
image-.png
image.png
image.png
// 貪心算法——0-1背包.cpp : 此文件包含 "main" 函數。程序執行將在此處開始并結束。
//
#include
#include
#include
using namespace std;

struct Item
{
int id;
float value;
float weight;
float v_w;
};
const int maxn = 1000;
bool isChosen[maxn];
vector- item;
bool cmp(Item a,Item b)
{
if (a.v_w > b.v_w)
return true;

else
return false;
}
void Knapsack_greedy(int n,int M)
{
int totw = 0;//記錄當前重量
for (int i = 0;i < n;i++)
{
if (totw + item[i].weight<=M)
{
isChosen[item[i].id] = true;
totw += item[i].weight;
}
}

}
int main()
{
int n;//物品數量
int M;//背包最大容量
cin >> n >> M;
float value, weight;
for (int i = 0;i < n;i++)
{
cin >> value >> weight;
item.push_back({ i,value,weight,value / weight });//存儲物品信息
}
sort(item.begin(), item.end(), cmp);
Knapsack_greedy(n, M);
for (int i = 0;i < n;i++)
{
if (isChosen[i])
{
cout <<"選擇物品為:"<< i+1 << " ";
}
}
return 0;
}