
廣州暨南大學圖書館3討論311回歸方程(3)與在原數據中剔除異常值(238,121)后用最小二乘法所得回歸方程Y40.33-比很接近,說明該方法較可靠。312若在原始數據中檢測到異常值,該值通過復查確屬錯誤應予以剔除。若不屬錯誤應予保留,用穩健估計方法研究,剔除則會損失信息。本文的計算結果是用Turbo語言在486DX機上編程計算得到的。數理統計與管理,1992,正確處理醫學科研中出現的可疑值1中國衛生統計,1992,631收稿日期:2000-09-26文章編號:(2001)中圖分類號:文獻標識碼:利用SPSS進行主成分回歸分析利用on、和等過程,結合線性回歸和主成分分析的基本原理,介紹了多重共線性診斷、主成分回歸分析過程和確定最佳方程的方法。關鍵詞:多重共線性診斷;主成分回歸分析在多變量分析中,常常采用最小二乘法擬合多重線性回歸模型。但是最小二乘估計有時會很不理想,造成這種情況的一個重要原因是矩陣X的列向量接近線性相關,這種自變量之間的近似線性關系我們稱為多重共線性,而多重共線性存在是我們求出的回歸系數的符號及其數值理理論不一致的主要原因。
本文利用通過主成分和線性回歸相結合的方法來解決多重共線性的問題1基本原理與計算方法111以應變量Y和全部自變量X進行逐步回歸,篩選出P個有統計學意義的自變量,并且診斷各自變量的多重共線性。112用P個自變量進行主成分分析,得到主成分矩陣和各主成分的累計方差百分比。113計算標化應變量和P個標化自變量,分別見式(1)和式式得到P個主成分的值。個自變量標準差,Ci個主成分,aij為主成分矩陣(Ci114從累計方差百分比85%所包括的主成分開始建立標化主成分回歸方程,再向后逐步增加主成分個數,得到m化主成分回歸方程中第i個標化偏回歸系數。115計算m個標化主成分回歸方程的殘差見式(5)參考較小殘差絕對值均數和較大累計方差百分比,的殘差絕對值。116把(3)代入最佳標化主成分回歸方程,整理后得標化線性回歸方程:’為標化線性回歸方程估計值,它與相應的標化主成分回歸方程估計值等價;標化偏回歸系數。117把標化線性回歸方程轉換成一般線性回歸方程。標化偏數理醫藥學雜志2001年第-.,Ltd..回歸系數轉換為偏回歸系數以及常數的計算公式為:bibi為一般線性回歸方程的第的離均差平方和,b0為一般線性回歸方程的常數。

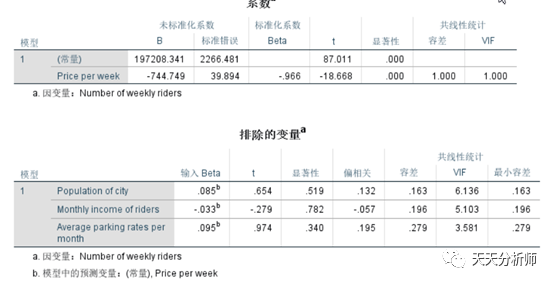
2應用實例例在1951~1998年間(缺乏1986和1969年的數據)貨運量(萬噸)為自變量X客運量(萬人)為自變量X有路面里程數(萬公里)為自變量X和無路面里程數(萬公里)為自變量過程的向后逐步法篩選變量和進行多重共線性診斷。對話框,把應變量Y放入全部自變量放入下拉菜單中,選擇)的自變量。在對話框,選擇、,其它為系統默認值。運行過程后,應變量Y和自變量X的均數標準差分別為2.35042.0428、730..0913、..68、54..5176。從相關矩陣得各自變量X之間的簡單相關系數分別為RX831。其它結果見表1表1回歸系數及其共線性統計量模型偏回歸系數04025..表2共線性診斷指標特征值條件指數方差百分比常數.使用過程,對自變量X進行主成分分析。

在對話框,把自變量X放入欄。在對話框spss主成分回歸步驟,選擇并在該欄內輸入3,其它為系數默認值。經過程運算后各種結果見表3。表3各主成分的特征值、方差百分比及其系數主成分特征值方差百分比累計方差百分比標化自變量74691.52391...使用過程,把應變量Y并求主成分C1、C2和C3在對話框,把betay輸入ion欄輸入在欄輸入標化自變量名分別為、betaX在欄輸入數學表達式分別為(X730.1911)1196.0913、.6854.1220)31.5176。計算主成分Ci在欄輸入主成分變量名分別為C1、C2和C3,在欄輸入數學表達式分別為4。不斷運行過程,工作數據表生成標化應變量、各標化自變量和主成分變量。
214使用過程進行主成分回歸分過程計算殘差和殘差絕對值。對話框,選擇betay放入選擇選擇C1放入’1C1。同理,擬合’3C3的操作僅僅是在欄放入的主成分變量有所增加,前者是放入C1和C2,后者是C1、C2和C3。擬合三個主成分回歸方程:121C3spss主成分回歸步驟,三個方程中的標化偏回歸系數的P05。對話框,把E1輸入欄作為殘差變量,在欄輸入betay-97C1)。同理,用表達式betay-158C2)和betay-121C3)可產生殘差變量E2和E3。在對話框,E1輸入欄作為殘差絕對值變量,在下拉菜單中,選擇ABS(把它放入。在對話框,把殘差絕對值變量Vo 1995- Disc Co., Ltd. All . 對值均數和標準差,見表4。

表4標化主成分回歸方程、殘差絕對值均數和標準差 標化主成分回歸方程 殘差絕對值均數標準差 31871.0732 32181.0643 32021.0618 215使用SPSS 過程, 計算L yy 在 ions 對話框, 選擇應變量Y 放入欄。在Op ions對話框, 選擇 Cro ss2p ion ,運行 過程產 187.788, 44701.175。 216把標化主成分回歸方程轉換為標化線性回歸方程, 然后 再轉換為一般線性回歸方程。 按較小平均絕對殘差和較大累計方差百分比的原則, 121C3。從表3可得: C1= 9508按(8)式計算bi 并按(9)式計算b0, 得一般線性回歸方 3討論進行多重線性回歸分析時, 出現結果與實際不符, 統計師 往往會懷疑是否存在多重共線性。本例經逐步回歸分析得b1 ,顯示車禍死亡率與機動車數量呈負相關, 結果 有悖常理。檢查是否存在共線性, 除了簡單相關系數之外 SPSS 還提供共線性統計量 )和方差膨脹因 個自變量與其它自變量的決定系數, 容差越小(接近0) 該自變量幾乎是其它自變量的線性組合。

V ()、條件指數( Index) 和自變量方差百分 比( Propo rt ion) 共線性的診斷指標 根據特征值的大小可以把自變量劃區分到不同維數() 當特征值接近0, 其對應的某些自變量呈高度相關, 該矩陣稱為“病態”。 條件指數是最大特征值與隨后特征值之比的平方根, 條件指 15表示可能存在共線性, 30表示有高度共線性。自變 量方差百分比由與特征值相聯系的主成分來解釋, 大條件指 數歸因于大方差的自變量, 因此, 擁有大方差的自變量是構成 相互高度相關的自變量。本例RX 25.233, 46.402, 和條件指數= 21. 362, 其特征值接近0 和條件指數> 15 有別于前三維的特征值和條件指數, 其對應 的自變量X 88和0199。這些 證據均支持自變量X 存在共線性。主成分分析可以把相關性較強的自變量綜合在同一主成 各主成分彼此獨立,使相關自變量變為相互無關主成 分。盡可能取小殘差絕對值和大累計方差百分比, 使能夠充分 利用原有的信息, 然后把主成分回歸方程轉換為線性回歸方 這樣,既克服了共線性的干擾和暴露本來真面目(本例經 主成分回歸分析, 把b1= 糾正為b1 明車禍死亡率與機動車數量呈正相關,符合客觀事實) 又不損失原有信息(本例最佳主成分回歸方程為: 121C3,其殘差絕對值均數與標準差為 158C2方程的殘差 絕對值均數與標準差基本一致, 其累計方差百分比為100%, 即利用全部原有信息)。
最佳標化主成分回歸方程中的B 均有統計學意義(P 的信息,可以間接說明標化線性回歸方程的b’1、b’3 有統計學意義,同理也可以推論一般線性回歸方程的b1、b3 b4均顯著。這樣, 即可以使用標化偏回歸系數b’i 作因素分析, 也可以使用一般線性回歸方程: 作預測。計算主成分Ci 因為其數學表達式為: Ci 而不能使用原始自變量X 。如果使用原始自變量X 計算 會導致各主成分之間全相關(R ci 利用SPSS進行主成分回歸分析是一種行之有效的方法。 它不但可以用多個共線性提標診斷每個自變量的共線性, 且可以解決共線性問題,同時絕大部分的計算過程由計算機 完成, 可以減少人工計算的繁瑣且保證結果無誤, 達到簡便、 快捷和準確的統計效果。 主成分回歸分析1中國衛生統計, 1991, 20~22.2方積乾(主編) 上海:上海 科技出版社, 1997, 295~301. 3劉潤幸(主編) 等 廣州:廣東人民出版社, 1999, 259~264. 4SPSS Inc. SPSS SA.SPSS Inc: 1997. 收稿日期: 2000- 10- 09 數理醫藥學雜志2001 年第14 1995- Disc Co., Ltd. All .