
一 、空間幾何體
(一) 空間幾何體的類型
1 多面體:由若干個平面多邊形圍成的幾何體。圍成多面體的各個多邊形叫做多面體的面,相鄰兩個面的公共邊叫做多面體的棱,棱與棱的公共點叫做多面體的頂點。
2 旋轉體:把一個平面圖形繞它所在的平面內的一條定直線旋轉形成了封閉幾何體。其中,這條直線稱為旋轉體的軸。
(二) 幾種空間幾何體的結構特征
1 、棱柱的結構特征
1.1 棱柱的定義:有兩個面互相平行,其余各面都是四邊形,并且每相鄰兩個四邊形的公共邊都互相平行,由這些面所圍成的幾何體叫做棱柱。
1.2 棱柱的分類
棱柱四棱柱平行六面體直平行六面體長方體正四棱柱正方體
性質:
Ⅰ、側面都是平行四邊形,且各側棱互相平行且相等;
Ⅱ、兩底面是全等多邊形且互相平行;
Ⅲ、平行于底面的截面和底面全等;
1.3 棱柱的面積和體積公式
S直棱柱表面 = c·h+ 2S底
V棱柱 = S底 ·h
2 、棱錐的結構特征
2.1 棱錐的定義
(1) 棱錐:有一個面是多邊形,其余各面是有一個公共頂點的三角形,由這些面所圍成的幾何體叫做棱錐。
(2)正棱錐:如果有一個棱錐的底面是正多邊形,并且頂點在底面的投影是底面的中心,這樣的棱錐叫做正棱錐。
2.2 正棱錐的結構特征
Ⅰ、 平行于底面的截面是與底面相似的正多邊形,相似比等于頂點到截面的距離與頂點到底面的距離之比;它們面積的比等于截得的棱錐的高與原棱錐的高的平方比;截得的棱錐的體積與原棱錐的體積的比等于截得的棱錐的高與原棱錐的高的立方比;
Ⅱ、 正棱錐的各側棱相等,各側面是全等的等腰三角形;
正棱錐側面積:
體積:
正四面體:
3 、棱臺的結構特征
3.1 棱臺的定義:用一個平行于底面的平面去截棱錐,我們把截面和底面之間的部分稱為棱臺。
3.2 正棱臺的結構特征
(1)各側棱相等,各側面都是全等的等腰梯形;
(2)正棱臺的兩個底面和平行于底面的截面都是正多邊形;
(3)正棱臺的對角面也是等腰梯形;
(4)各側棱的延長線交于一點。
4 、圓柱的結構特征
4.1 圓柱的定義:以矩形的一邊所在的直線為旋轉軸,其余各邊旋轉而形成的曲面所圍成的幾何體叫圓柱。
4.2 圓柱的性質
(1)上、下底及平行于底面的截面都是等圓;
(2)過軸的截面(軸截面)是全等的矩形。
4.3 圓柱的側面展開圖:圓柱的側面展開圖是以底面周長和母線長為鄰邊的矩形。
4.4 圓柱的面積和體積公式
S圓柱側面 = 2π·r·h (r為底面半徑如圖是一個空間幾何體的三視圖,h為圓柱的高)
S圓柱全 = 2π r h + 2π r2
V圓柱 = S底h = πr2h
5、圓錐的結構特征
5.1 圓錐的定義:以直角三角形的一直角邊所在的直線為旋轉軸,其余各邊旋轉而形成的曲面所圍成的幾何體叫做圓錐。
5.2 圓錐的結構特征
(1) 平行于底面的截面都是圓,截面直徑與底面直徑之比等于頂點到截面的距離與頂點到底面的距離之比;
(2)軸截面是等腰三角形;
(3)母線的平方等于底面半徑與高的平方和:
l2 = r2 + h2
5.3 圓錐的側面展開圖:圓錐的側面展開圖是以頂點為圓心,以母線長為半徑的扇形。
6、圓臺的結構特征
6.1 圓臺的定義:用一個平行于底面的平面去截圓錐,我們把截面和底面之間的部分稱為圓臺。
6.2 圓臺的結構特征
⑴ 圓臺的上下底面和平行于底面的截面都是圓;
⑵ 圓臺的截面是等腰梯形;
⑶ 圓臺經常補成圓錐,然后利用相似三角形進行研究。
6.3 圓臺的面積和體積公式
S圓臺側 = π·(R + r)·l (r、R為上下底面半徑)
S圓臺全 = π·r2 + π·R2 + π·(R + r)·l
V圓臺 = 1/3 (π r2 + π R2 + π r R) h (h為圓臺的高)
7 球的結構特征
7.1 球的定義:以半圓的直徑所在的直線為旋轉軸,半圓旋轉一周形成的旋轉體叫做球體。空間中,與定點距離等于定長的點的集合叫做球面,球面所圍成的幾何體稱為球體。

7-2 球的結構特征
⑴ 球心與截面圓心的連線垂直于截面;
⑵ 截面半徑等于球半徑與截面和球心的距離的平方差:r2 = R2 – d2
★7-3 球與其他多面體的組合體的問題
球體與其他多面體組合,包括內接和外切兩種類型,解決此類問題的基本思路是:
⑴ 根據題意,確定是內接還是外切,畫出立體圖形;
⑵ 找出多面體與球體連接的地方,找出對球的合適的切割面,然后做出剖面圖;
⑶ 將立體問題轉化為平面幾何中圓與多邊形的問題;
⑷ 注意圓與正方體的兩個關系:球內接正方體,球直徑等于正方體對角線;
球外切正方體,球直徑等于正方體的邊長。
7-4 球的面積和體積公式
S球面 = 4 π R2 (R為球半徑)
V球 = 4/3 π R3
(三)空間幾何體的表面積與體積
空間幾何體的表面積
棱柱、棱錐的表面積:各個面面積之和
圓柱的表面積 :
圓錐的表面積:
圓臺的表面積:
球的表面積:
扇形的面積公式
空間幾何體的體積
柱體的體積 :
錐體的體積 :
臺體的體積 :
球體的體積:
(四)空間幾何體的三視圖和直觀圖
正視圖:光線從幾何體的前面向后面正投影,得到的投影圖。
側視圖:光線從幾何體的左邊向右邊正投影,得到的投影圖。
俯視圖:光線從幾何體的上面向右邊正投影,得到的投影圖。
★畫三視圖的原則:
正俯長相等、正側高相同、俯側寬一樣
注:球的三視圖都是圓;長方體的三視圖都是矩形
直觀圖:斜二測畫法
斜二測畫法的步驟:

(1)平行于坐標軸的線依然平行于坐標軸;
(2)平行于y軸的線長度變半,平行于x,z軸的線長度不變;
(3)畫法要寫好
用斜二測畫法畫出長方體的步驟:(1)畫軸(2)畫底面(3)畫側棱(4)成圖
二 、點、直線、平面之間的關系
(一)、立體幾何網絡圖:
1、線線平行的判斷:
(1)、平行于同一直線的兩直線平行。
(3)、如果一條直線和一個平面平行,經過這條直線的平面和這個平面相交,那么這條直線和交線平行。
(6)、如果兩個平行平面同時和第三個平面相交,那么它們的交線平行。
(12)、垂直于同一平面的兩直線平行。
2、線線垂直的判斷:
(7)、在平面內的一條直線,如果和這個平面的一條斜線的射影垂直,那么它也和這條斜線垂直。
(8)、在平面內的一條直線,如果和這個平面的一條斜線垂直,那么它和這條斜線的射影垂直。
(10)、若一直線垂直于一平面,這條直線垂直于平面內所有直線。
補充:一條直線和兩條平行直線中的一條垂直,也必垂直平行線中的另一條。
3、線面平行的判斷:
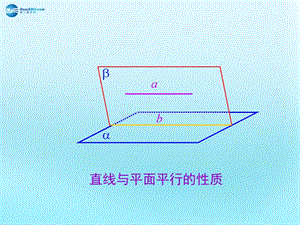
(2)、如果平面外的一條直線和平面內的一條直線平行,那么這條直線和這個平面平行。
(5)、兩個平面平行,其中一個平面內的直線必平行于另一個平面。
判定定理:
性質定理:
★判斷或證明線面平行的方法
⑴ 利用定義(反證法):
⑵ 利用判定定理:線線平行
線面平行 (用于證明);
⑶ 利用平面的平行:面面平行
線面平行 (用于證明);
⑷ 利用垂直于同一條直線的直線和平面平行(用于判斷)。
2 線面斜交和線面角:
2.1 直線與平面所成的角(簡稱線面角):若直線與平面斜交,則平面的斜線與該斜線在平面內射影的夾角θ。
2.2 線面角的范圍:θ∈[0°,90°]
注意:當直線在平面內或者直線平行于平面時,θ=0°;
當直線垂直于平面時,θ=90°
4、線面垂直的判斷:
⑼如果一直線和平面內的兩相交直線垂直,這條直線就垂直于這個平面。
⑾如果兩條平行線中的一條垂直于一個平面,那么另一條也垂直于這個平面。
⒁一直線垂直于兩個平行平面中的一個平面,它也垂直于另一個平面。
⒃如果兩個平面垂直,那么在—個平面內垂直于交線的直線必垂直于另—個平面。
判定定理:
性質定理:(1)若直線垂直于平面,則它垂直于平面內任意一條直線。
(2)垂直于同一平面的兩直線平行。
★判斷或證明線面垂直的方法
⑴ 利用定義,用反證法證明。
⑵ 利用判定定理證明。
⑶ 一條直線垂直于平面而平行于另一條直線,則另一條直線也垂直與平面。
⑷ 一條直線垂直于兩平行平面中的一個,則也垂直于另一個。
⑸ 如果兩平面垂直,在一平面內有一直線垂直于兩平面交線,則該直線垂直于另一平面。
★1.5 三垂線定理及其逆定理
⑴ 斜線定理:從平面外一點向這個平面所引的所有線段中, 斜線相等則射影相等,斜線越長則射影越長,垂線段最短。
⑵ 三垂線定理及其逆定理
已知PO⊥α,斜線PA在平面α內的射影為OA,a是平面
α內的一條直線。
① 三垂線定理:若a⊥OA,則a⊥PA。即垂直射影則垂直斜線。
② 三垂線定理逆定理:若a⊥PA,則a⊥OA。即垂直斜線則垂直射影。
⑶ 三垂線定理及其逆定理的主要應用
① 證明異面直線垂直;
② 作出和證明二面角的平面角;
③ 作點到線的垂線段。
5、面面平行的判斷:
⑷一個平面內的兩條相交直線分別平行于另一個平面,這兩個平面平行。
⒀垂直于同一條直線的兩個平面平行。
6、面面垂直的判斷:
⒂一個平面經過另一個平面的垂線,這兩個平面互相垂直。
判定定理:
性質定理:
(二)、其他定理:
(1)確定平面的條件:①不公線的三點;②直線和直線外一點;③相交直線;
(2)直線與直線的位置關系: 相交 ; 平行 ; 異面 ;
直線與平面的位置關系: 在平面內 ; 平行 ; 相交(垂直是它的特殊情況) ;
平面與平面的位置關系: 相交 ;; 平行 ;

(3)等角定理:如果兩個角的兩邊分別平行且方向相同,那么這兩個角相等;
如果兩條相交直線和另外兩條相交直線分別平行,那么這兩組直線所成的銳角(或直角)相等;
(4)射影定理(斜線長、射影長定理):從平面外一點向這個平面所引的垂線段和斜線段中,射影相等的兩條斜線段相等;射影較長的斜線段也較長;反之,斜線段相等的射影相等;斜線段較長的射影也較長;垂線段比任何一條斜線段都短。
(5)最小角定理:斜線與平面內所有直線所成的角中最小的是與它在平面內射影所成的角。
(6)異面直線的判定:
①反證法;
②過平面外一點與平面內一點的直線,和平面內不過該點的直線是異面直線。
(7)過已知點與一條直線垂直的直線都在過這點與這條直線垂直平面內。
(8)如果—直線平行于兩個相交平面,那么這條直線平行于兩個平面的交線。
(三)、唯一性定理:
(1)過已知點如圖是一個空間幾何體的三視圖,有且只能作一直線和已知平面垂直。
(2)過已知平面外一點,有且只能作一平面和已知平面平行。
(3)過兩條異面直線中的一條能且只能作一平面與另一條平行。
四、空間角的求法:(所有角的問題最后都要轉化為解三角形的問題,尤其是直角三角形)
(1)異面直線所成的角:通過直線的平移,把異面直線所成的角轉化為平面內相交直線所成的角。異面直線所成角的范圍:
(2)線面所成的角:①線面平行或直線在平面內:線面所成的角為
; ②線面垂直:線面所成的角為
③斜線與平面所成的角:范圍;即也就是斜線與它在平面內的射影所成的角。
線面所成的角范圍
(3)二面角:關鍵是找出二面角的平面角。方法有:①定義法;②三垂線定理法;③垂面法;
五、距離的求法:
(1)點點、點線、點面距離:點與點之間的距離就是兩點之間線段的長、點與線、面間的距離是點到線、面垂足間線段的長。求它們首先要找到表示距離的線段,然后再計算。
注意:求點到面的距離的方法:
①直接法:直接確定點到平面的垂線段長(垂線段一般在二面角所在的平面上);
②轉移法:轉化為另一點到該平面的距離(利用線面平行的性質);
③體積法:利用三棱錐體積公式。
(2)線線距離:關于異面直線的距離,常用方法有:
①定義法,關鍵是確定出的公垂線段;
②轉化為線面距離,即轉化為與過而平行于的平面之間的距離,關鍵是找出或構造出這個平面;③轉化為面面距離;
(3)線面、面面距離:線面間距離面面間距離與線線間、點線間距離常常相互轉化;
六、常用的結論: