
今天給大家介紹的是多元線性回歸、指數擬合和非線性曲面擬合。一、多元線性回歸多元線性回歸用于分析多個自變量與一個因變量之間的線性關系。下式為一般多元線性方程。Y=A+B1X1+B2X2…+在進行多元線性回歸時,需將工作表中一列設置為因變量(Y),將其他的設置為自變量(X1,X2,X3,…,Xn)。實例演示:(1)導入要擬合的數據集,如圖1所示。
圖1 原始數據(2)選擇執行菜單命令→→ ,進行多元線性回歸,系統會彈出 窗口,如圖2所示。
圖 窗口在 對話框中,設置因變量(Y)和自變量(X1,X2,X3 …),如圖3所示,單擊OK按鈕確定。
圖3 設置因變量和自變量(3)根據輸出設置自動生成了具有專業水準的多元線性回歸分析報表,如圖4所示。
圖4 多元線性回歸擬合報告擬合函數:Y=-0.03356+5.-2.+1.相關系數:0.98709二、指數擬合指數擬合可分為指數衰減擬合和指數增長擬合,指數函數有一階函數和高階函數。實例示范:(1)導入數據,工作表如圖5所示。
圖5 指數擬合原始數據表(2)選中數據中的 A(X)、B(Y)列繪制散點圖。
選擇菜單命令→→ Fit,打開“NLFit”對話框。
此時origin數據表轉換矩陣,在“”下拉列表框中,給出了用一階指數衰減函數的擬合,如圖6所示。如果需要更改指數衰減函數的階數,可以在“”下拉列表框中進行選擇。
圖6 NLFit對話框下“”下拉列表單擊“NLFit”對話框的“”標簽,選擇對象參數性質的設置。如圖7所示,將y0和A1設置為常數。
圖7“NLFit”對話框的“”標簽(3)該對話框的下半部分,如圖8所示。單擊不同的標簽可以分別看到擬合效果、擬合函數和其他信息。圖8和圖9分別為擬合效果圖和擬合函數。

圖8“NLFit”對話框下半部分效果圖
圖9 “NLFit”對話框下半部分“”下拉列表
圖10“NLFit”對話框下半部分“ Curve”下拉列表(4)單擊“Fit”按鈕,完成對數據用一階指數衰減函數的擬合,根據輸出設置自動生成擬合參數分析報表和擬合數據工作表。如圖11為擬合曲線所示。圖12為輸出分析報告表。
圖11 一階衰減指數函數對數據擬合圖形

圖12 分析報告表三、非線性曲面擬合非線性曲面擬合是通過內置的表面擬合函數可以完成對三維數據的擬合。非線性曲面擬合操作與非線性曲線擬合基本相同。如果擬合數據是工作表數據,需要工作表有XYZ列數據,選中工作表中XYZ列數據,選擇菜單命令,即可完成非線性曲面擬合;如果擬合數據是矩陣工作表數據,選中矩陣工作表中數據,選擇菜單命令→ Fit,即可完成非線性曲面擬合。
圖13 矩陣工作表數據非線性曲面擬合
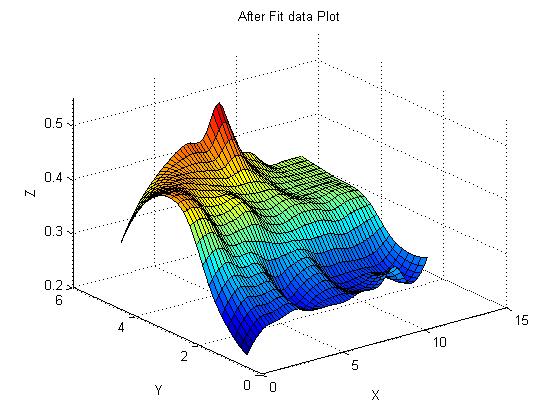
圖14矩陣工作表數據非線性曲面擬合報表如果對三維曲面進行擬合,該三維曲面必須采用矩陣繪制,其擬合過程與上面一樣origin數據表轉換矩陣,也是執行菜單命令一→ Fit。因為曲面擬合有兩個自變量,因此散點圖無法表示平面的殘差,必須采用輪廓圖。下面通過以實例數據文件轉換的矩陣,來說明非線性曲面擬合。(1)導入數據文件,并將其轉換為矩陣工作表,如圖15所示。根據轉換后的矩陣表繪出圖形如圖16所示。
圖15 原始數據轉化為矩陣工作表
圖16繪制圖形(2)將圖16設置為當前窗口,執行菜單命令→→ Fit,打開NLFit對話框,選擇“”曲面函數,如圖17所示。
圖17 打開NLFit頁面(3)單擊Fit按鈕,完成曲面擬合,擬合得到的數據存放在新建的工作表中,如圖18所示。
圖18非線性擬合數據報表把參數代入函數即可得到擬合函數。這兩篇都是利用內置的函數進行曲線擬合,雖然 in 內置的函數有200多個,然而實際使用時,我們會發現自己的擬合函數并不在內置中,這樣就需要自定義函數進行曲線擬合。這個內容留待下次介紹,敬請期待!