
《數(shù)字信號(hào)處理習(xí)題答案及實(shí)驗(yàn)詳解》由會(huì)員分享,可在線閱讀,更多相關(guān)《數(shù)字信號(hào)處理習(xí)題答案及實(shí)驗(yàn)詳解(21頁(yè)珍藏版)》請(qǐng)?jiān)谧x根文庫(kù)上搜索。
1、 1 第一章 參考答案: 1 (1) 0 221 4 3 3 7 ,有理數(shù),所以周期為 14 (2) 0 22 12 1 6 ,無(wú)理數(shù),非周期 2 (1) 1 2 3 3 2 1 (2) 當(dāng) 0 n 時(shí) 1 1 y( ) 0.5 2 2 3 nmm n m n 當(dāng) 1 n 時(shí) 4 y( ) 0.5 2 2 3 n nmm n m n 3 線性,時(shí)變 4 (1)因果,不穩(wěn)定 (2)非因果,穩(wěn)定 5 單位抽樣響應(yīng): 1 1 () ( 1 ) () 2 n hn un n 2 1 2 (n m) 1 y( ) ( ) * ( ) 1 1 2 (n 1) e ( ) 1 2 2 n jn m jj n
2、 j n j m nx nh n e ee uu n e 第二章 1 求下列序列的 Z 變換并畫出零、極點(diǎn)圖。 (1) x( ) n na (2) 0 x( ) sin( ) 0 nn nn 2 分別用乘除法、留數(shù)定理和部分分式法求下列 X(Z)的反變換。 1 X(z) 1 za z az a 答案: 11 1 x( ) ( ) (a ) (n 1) n nn u aa a 3 4 3 有一信號(hào) y(n),它與另兩個(gè)信號(hào) x1(n)和 x2(n)的關(guān)系是: 12 () ( n3 ) * x( 1 ) yn x n 其中數(shù)字信號(hào)處理matlab版答案, 12 11 x() () , x() () 23 nn nu nnu n
3、 利用 Z變換性質(zhì)求 y(n)的 Z變換 Y(Z)。 實(shí)驗(yàn)2-1 離散系統(tǒng)的分析的基本理論 實(shí)驗(yàn)?zāi)康模杭由顚?duì)離散系統(tǒng)基本理論和方法的理解 1 一線性移不變離散時(shí)間系統(tǒng)的單位抽樣響應(yīng)為 ( ) (1 0.3 0.6 ) ( ) nn hn un (1) 求該系統(tǒng)的轉(zhuǎn)移函數(shù) () H z ,并畫出其零-極點(diǎn)圖; (2) 寫出該系統(tǒng)的差分方程。 5 解: (1)系統(tǒng)的轉(zhuǎn)移函數(shù)是是其單位抽樣響應(yīng)的Z變換,因此 12 12 123 1113 3 . 81 . 0 8 () 1 1 0.3 1 0.6 (1 )(1 0.3 )(1 0.6 ) 3 3.8 1.08 1 1 1.9 1.08
4、0.18 zz Hz zz Z zzz 系統(tǒng)的零極點(diǎn)圖如下圖所示: B=3,-3.8,1.08; A=1,-1.9,1.08,-0.18; Z,P,K=tf2zp(B,A); (B,A) Z = 0,0.8361,0.4306 P =1.0000, 0.6000,0.3000 (2) 由于 12 123 ( ) 3 3.8 1.08 () ( ) 1 1.9 1.08 0.18 Yz z z Hz Xz z z z 所以系統(tǒng)的差分方程: ( ) 1.9 ( 1) 1.08 ( 2) 0.18 ( 3) 3 ( ) 3.8 ( 1) 1.08 ( 2) yn yn yn

5、 yn xn xn xn 2 已知用下列差分方程描述的一個(gè)線性移不變因果系統(tǒng) ()(1 )(2 )(1 ) yn yn yn xn 6 (a) 求這個(gè)系統(tǒng)的系統(tǒng)函數(shù) () () () Yz Hz X z ,畫出 () H z 的零-極點(diǎn)圖并指出其 收斂區(qū)域; (b) 求此系統(tǒng)的單位抽樣響應(yīng); 解:(a) 1 12 () () () 1 Yz z Hz Xz z z |Z|1.618 B=0,1; A=1,-1,-1; Z,P,K=tf2zp(B,A); (B,A); Z =0 P = -0.6180,1.6180 (b) B=0,1; A=1,-1,-1; h,t=impz(B,A
6、,50); Stem(t,h,.); 7 3 一個(gè)離散時(shí)間系統(tǒng)的一對(duì)共軛極點(diǎn): 4 1 0.8 j p e , 4 2 0.8 j pe ,在原點(diǎn)有二 階重零點(diǎn)。 (1) 寫出該系統(tǒng)的轉(zhuǎn)移函數(shù) () H z ,畫出零-極點(diǎn)圖; (2) 試用零-極點(diǎn)分析的方大致畫出其幅頻響應(yīng)(02) ; (3) 若輸入信號(hào) () () xnu n ,并且系統(tǒng)有初始條件 (2 ) (1 )1 yy ,求該系統(tǒng) 的輸出 () y n 解: (1)依題意: 2 12 11 12 44 11 () 0.8 () () 1 1 . 1 30 . 6 4 (1 0.8 )(1 0.8 ) jj z Hz z zpzp z
7、z ez ez B=1; A=1,-1.13,0.64; Z,P,K=tf2zp(B,A); (B,A); 8 (2) 由H(z)的表達(dá)式,不難求出, 當(dāng)w=0時(shí), 0 ( ) 1/ 0.51 2; j He 當(dāng)w=時(shí), ( ) 1/ 2.77 0.36; j He 當(dāng)w=/4時(shí), 4 ( ) 1/ 0.256 4 j He ,峰值。 B=1; A=1,-1.13,0.64; H,w=freqz(B,A,256,whole,1); (1); (2,1,1); plot(w,abs(H) (2,1,2); plot(w,angle(H) 9 (
8、3)此處給出的系統(tǒng)初始條件不為零,因此系統(tǒng)的輸出由兩部分組成,一是零輸 入解,二是零狀態(tài)解。 求零輸入解: 1 1 1 12 0 () () 0.49 0.64 () , 1 1.13 0.64 () N km km k oi N k k akz ymz z Yz zz akz /4 /4 ( ) (0.245 0.3206)0.8 ( ) (0.245 0.3206)0.8 ( ) nj n nj n oi y n j eu n j eu n 求零狀態(tài)解: 由 () () xnu n 可知, 1 1 () 1 Xz z 12 1 () 11 . 1 3 0 . 6 4 Hz zz 1 11
9、44 1/ 4 1/ 4 1 11 () ()() 1 (1 0. 8 )(1 0. 8 ) 1.9608 0.4804 0.6286 0.4804 0.6286 1 1 0.8 1 0.8 jj jj Yz HzXz z ez ez jj ze ze z 10 /4 /4 0 ( ) 1.9608 ( ) ( 0.4804 0.6286)0.8 ( ) ( 0.4804 0.6286)0.8 ( ) nj n nj n s ynu n j eu n j eu n 系統(tǒng)輸出: 0 /4 /4 () () () 1.9608 ( ) (0.2354 0.308)0.8 ( ) (0.2354 0

10、.308)0.8 ( ) os i nj n nj n yn y n y n un j e un j e un y0=1 1; xic=(b,a,y0); N=100;n=0:N-1;xn=ones(1,N); yn=(b,a,xn,xic); plot(n,yn); 實(shí)驗(yàn)2-2 離散系統(tǒng)的差分方程、沖激響應(yīng)和卷積分析 實(shí)驗(yàn)內(nèi)容:編制程序求解下列兩個(gè)系統(tǒng)的單位沖激響應(yīng)和階躍響應(yīng),并繪出其圖 形。 1 2 125 . 0 1 75 . 0 n x n x n y n y n y 4 3 2 1 25 . 0 n x n x n x n x n y 實(shí)驗(yàn)要求:給出理論計(jì)算結(jié)
11、果和程序計(jì)算結(jié)果并討論。 11 解:(1) 1 2 125 . 0 1 75 . 0 n x n x n y n y n y 轉(zhuǎn)移函數(shù)為: 1 12 1 ( ) , 0.5 1 0.75 0.125 z Hz z zz 利用r,p,k=(num,den),則 11 65 () 1 0.5 1 0.25 Hz zz , 單位抽樣響應(yīng)(沖激響應(yīng))為: ( ) 6( 0.5) ( ) 5( 0.25) ( ) nn hn un un 即 (0) 1, (1) 1.75, (2) 1.1875, (3) 0.6719, (4) 0.3555,. hh h h h 階躍響應(yīng)為: 0 (
12、) , , 0 mm yn xn hn xmhn m hn mn mm 即 (0) 1, (1) 0.75, (2) 0.4375, (3) 0.2344, (4) 0.1211,. yy y y y 利用函數(shù) h=impz(b,a,N)和 y=(b,a,x)分別繪出沖激和階躍響應(yīng): b=1,-1; a=1,0.75,0.125; x=ones(1,100); h=impz(b,a,100); y1=(b,a,x); (1) (2,1,1); plot(h); (2,1,2); plot(y1); 12 (2) 4 3 2 1 2
13、5 . 0 n x n x n x n x n y 轉(zhuǎn)移函數(shù)為: 1234 ( ) 0.25( ) Hz z z z z 沖激響應(yīng)為: ( ) 0.25( ( 1) ( 2) ( 3) ( 4) hn n n n n 即 (0) 0, (1) 0.25, (2) 0.25, (3) 0.25, (4) 0.25, ( ) 0,( 4) hhhhh h nn 其余 階躍響應(yīng)為: 0 ( ) , , 0 mm yn xn hn xmhn m hn mn mm 即 (0) 0, (1) 0.25, (2) 0.5, (3) 0.75, ( ) 1,( 3) yyyy y nn 其余 利用函數(shù)h=im
14、pz(b,a,N)和y=(b,a,x)分別繪出沖激和階躍響應(yīng) b=0,0.25,0.25,0.25,0.25; a=1; x=ones(1,100); h=impz(b,a,100);y=(b,a,x) (1) (2,1,1); stem(h,.); (2,1,2); plot(y,.); 13 實(shí)驗(yàn)2-3 離散系統(tǒng)的頻率響應(yīng)分析和零、極點(diǎn)分布 實(shí)驗(yàn)?zāi)康模杭由顚?duì)離散系統(tǒng)的頻率響應(yīng)分析和零、極點(diǎn)分布的概念理解。 在中,可以用函數(shù)z,p,K=tf2zp(num,den)求得有理分式形式的 系統(tǒng)轉(zhuǎn)移函數(shù)的零、極點(diǎn),用函數(shù) z
15、plane(z,p)繪出零、極點(diǎn)分布圖;也可以 用函數(shù)(num,den)直接繪出有理分式形式的系統(tǒng)轉(zhuǎn)移函數(shù)的零、極點(diǎn)分 布圖。 另外,在中,可以用函數(shù) r,p,k=(num,den)完成 部分分式展開計(jì)算;可以用函數(shù)sos=(z,p,K)完成將高階系統(tǒng)分解為 2階系統(tǒng)的串聯(lián)。 實(shí)驗(yàn)內(nèi)容:求系統(tǒng) 12345 12345 0.0528 0.797 0.1295 0.1295 0.797 0.0528 () 1 1.8107 2.4947 1.8801 0.9537 0.2336 zzzzz Hz zzzzz 的零、極點(diǎn)和幅度頻率響應(yīng)。 實(shí)驗(yàn)要求:
16、編程實(shí)現(xiàn)系統(tǒng)參數(shù)輸入,繪出幅度頻率響應(yīng)曲線和零、極點(diǎn)分布圖。 解:利用函數(shù)z,p,k=tf2zp(b,a)求出零極點(diǎn): b=0.0528,0.797,0.1295,0.1295,0.797,0.0528; 14 a=1,-1.8107,2.4947,-1.8801,0.9537,-0.2336; z,p,k=tf2zp(b,a); (b,a) h,w=freqz(b,a,256,whole,1); (2) (1,2,1);plot(w,abs(h); (1,2,2);plot(w,(angle(h) z= -14.9370 p=
17、0.2788 + 0.8973i k= 0.0528 0.4546 + 0.8907i 0.2788 - 0.8973i 0.4546 - 0.8907i 0.3811 + 0.6274i -1.0000 0.3811 - 0.6274i -0.0669 0.4910 15 第三章 習(xí)題部分: 1 設(shè)信號(hào)x(n0=1,2,3,4,通過(guò)系統(tǒng)h(n)=4,3,2,1, n=0,1,2,3; (1)求系統(tǒng)的輸出y(n)=x(n)*h(n); (2)試用循環(huán)卷積計(jì)算y(n); (3)簡(jiǎn)述通過(guò)DFT來(lái)計(jì)算y(n)的思路。 解 (1)y(n)=4,11,20,30,20,11,4 (2)通過(guò)圓卷積(DFT
18、 算法)求系統(tǒng)的輸出過(guò)程如下: 取 8 7 1 4 4 1 2 1 N N L 令 7 4 , 0 3 0 ), ( ) ( n n n x n x , 7 4 , 0 3 0 ), ( ) ( n n n h n h ) , ( ) ( , ) , ( ) ( L h FFT k H L x FFT k X ) ( ) ( ) ( k H k X k Y 16 ) ( ) ( Y IFFT n y 2 設(shè)有兩個(gè)序列為: () , 0 5 () 0, xn n xn 其他 , () , 0 1 4 () 0, yn n yn 其他 ,各 作15點(diǎn)的DFT, 然后將兩個(gè)DFT相乘, 再求乘積的I
19、DFT, 設(shè)所得結(jié)果為f(n), 問(wèn)f(n)的哪些點(diǎn)對(duì)應(yīng)于x(n)*y(n)應(yīng)該得到的點(diǎn)。 答:5-14 3. 有一頻譜分析儀用的FFT處理器,其抽樣點(diǎn)數(shù)必須是2的整數(shù)冪。假定沒有 采用任何特殊的數(shù)據(jù)處理措施,已給條件為: (1)頻率分辨力10Hz (2)抽樣時(shí)間間隔為0.1ms,試確定以下參量: (1)最小記錄長(zhǎng)度Tp; (2)所允許處理的信號(hào)的最高頻率; (3)在一個(gè)記錄中的最少點(diǎn)數(shù)N。 解: 頻率分辨率 11 10 s sp f f Hz NN Tt ,所以 0.1 p ts 設(shè)采樣頻率為 s f ,則根據(jù)采樣定理,有 max 11 1 5 22 s s f fK H z T 一個(gè)記錄中
20、的最少點(diǎn)數(shù) 10000 1000 10 s f N f 考慮使用 FFT 算法,取 N=1024 4 已知x(n)是長(zhǎng)為N的有限長(zhǎng)序列, () () XkD F Tx n , 現(xiàn)將長(zhǎng)度擴(kuò)大r倍,得 長(zhǎng)度為rN的有限長(zhǎng)序列 () , 0 1 () 0, 1 xn n N yn Nnr N , 求: () DFT y n 與 () X k 的關(guān)系。 已知 x(n)是長(zhǎng)為 N 的有限長(zhǎng)序列,X(K)=DFTx(n),現(xiàn)將 x(n)的每?jī)牲c(diǎn)之間補(bǔ)進(jìn) r - 1個(gè)零點(diǎn),得到一長(zhǎng)為r N的有限長(zhǎng)序列y ( n ), 17 n N i ir n r n x n y 其他 , 0 1 , , 0 , ), /
21、 ( ) ( 求:DFTy(n)與 X(k)的關(guān)系。 解: 1 0 11 00 () () () () () () N kn N n k rN N n kn r rN N nn Xk xnW k Yk ynW xnW X r ) ( ) ( ) ( ) ( ) ( ) ( 1 0 1 0 1 0 k X W i x W n y k Y W n x k X N i ki N rN n kn rN N n kn N 5 試畫出 N=16 點(diǎn)基 2-按時(shí)間抽取的 FFT 運(yùn)算流圖,說(shuō)明共有多少級(jí),每級(jí)有 多少個(gè)蝶形單元,并寫出每一級(jí)的旋轉(zhuǎn)因子。 50 , 5 . 512 () , 如果一臺(tái)通用計(jì)算機(jī)
22、的速度為平均每次復(fù)乘需 每次復(fù)加 用它來(lái)計(jì)算 點(diǎn) 的 問(wèn)直接計(jì)算需要多少時(shí)間,用 運(yùn)算需要多少時(shí)間。 us us DFT x n FFT 答:共有4級(jí),每級(jí)都有8個(gè)蝶形單元 18 2 2 2 *50 13.11( ) 1)*5 1.308( ) 512 14.418( ) log *50 256*9*50 0.1152( ) 2 log *5 512*9*5 0.02304( ) 直接計(jì)算 需要復(fù)乘次數(shù) 直接計(jì)算 需要復(fù)加次數(shù) ( 直接計(jì)算 點(diǎn) 共需要時(shí)間 用 運(yùn)算需要復(fù)乘次數(shù) 用 運(yùn)算需要復(fù)加次數(shù) N N DFT N s DFT N N s DFT s N FFT s FFT N s 512
23、 0.13824( ) 用 來(lái)計(jì)算 點(diǎn)共需時(shí)間 FFT s 實(shí)驗(yàn)內(nèi)容與指導(dǎo) 實(shí)驗(yàn) 1 抽樣定理的實(shí)驗(yàn)體會(huì) 實(shí)驗(yàn)?zāi)康模杭由顚?duì)抽樣定理的理解 實(shí)驗(yàn)內(nèi)容:任選一個(gè)下述五個(gè)連續(xù)時(shí)間信號(hào) () x t 轉(zhuǎn)換成離散時(shí)間信號(hào)() s x nT ,在 計(jì)算機(jī)上繪出() s x nT 的圖形。 1/ s s f T 為抽樣頻率。自行依次選取不同的抽樣頻 率,如 0000 0.5 , ,2 ,5 s f ffff 等,以體會(huì)對(duì)不同的信號(hào),或者同一信號(hào)采用多大的 抽樣頻率較為合適。 (1) 工頻信號(hào): 10 () s i n ( 2 ) xtA f t , 220 A , 0 50 f Hz (2) 衰減正弦信號(hào):
24、 20 () s i n ( 2 ) t xtA e f t , 2 A , 0.5 , 0 2 f Hz (3) 諧波信號(hào): 3 20 1 () s i n ( 2 ) i i xtAf i t , 1 1 A , 2 0.5 A , 3 0.2 A , 0 5 f Hz (4) (哈明)窗: 40 ( ) 0.54 0.46cos(2 ) xtf t , 0 f 由同學(xué)自選給定。 (5) sinc函數(shù): 5 sin( ) () t xt t , 2 f , 10 f Hz 實(shí)驗(yàn) 2 離散信號(hào)的 DTFT 和 DFT 實(shí)驗(yàn)?zāi)康模杭由顚?duì)離散信號(hào)的 DTFT 和 DFT 的及其相互
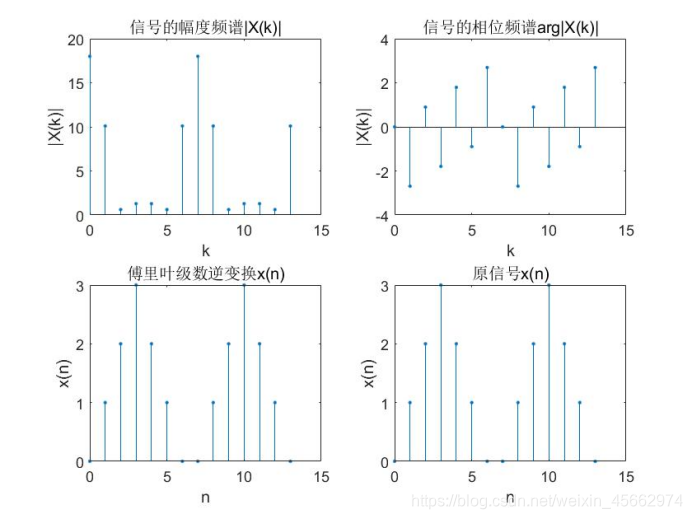
25、關(guān)系的理解。 實(shí)驗(yàn)內(nèi)容: 分別計(jì)算16點(diǎn)序列 15 0 , 16 5 cos ) ( n n n x 的16點(diǎn)和32點(diǎn)DFT, 繪出幅度譜圖形,并繪出該序列的DTFT圖形。 19 實(shí)驗(yàn)要求:討論 DTFT 和 DFT 之間的相互關(guān)系。說(shuō)明實(shí)驗(yàn)產(chǎn)生的現(xiàn)象的原因。 實(shí)驗(yàn) 3 正弦信號(hào)抽樣的實(shí)驗(yàn) 給定信號(hào) 00 () s i n ( 2 ) , 5 0 xtf t fH z ,現(xiàn)對(duì) x(t)抽樣,設(shè)抽樣點(diǎn)數(shù) N=16. 我們 知道正弦信號(hào)的頻譜是在 0 f 處的 函數(shù),將 x(t)抽樣變成 x(n)后,若抽樣率及 數(shù)據(jù)長(zhǎng)度 N取得合適, 那么 x(n)的 DFT 也應(yīng)是在 50Hz 處的 函數(shù), 由
26、 定理,有 1 2 2 50 0 2 () N tf n E xn X E N 50 X 表示 x(n)的 DFT 在 50Hz 處的譜線,若上式不等,說(shuō)明 X(k)在頻域有泄 露。給定以下抽樣頻率(a) 100 s f Hz , (a) 150 s f Hz , (c) 200 s f Hz , (1)分別得到 x(n)及計(jì)算其 X(k),并用 定理研究其泄露情況; (2)當(dāng)取 200 s f Hz ,N=16 時(shí),在抽樣點(diǎn)后面再補(bǔ) N個(gè)零,得到 () x n ,這時(shí) () x n 是 32點(diǎn)序列,求 () x n 的 DFT () X k ,觀察正弦信號(hào)
27、補(bǔ)零的影響。 (3)觀察抽樣得到 x(n)及 X(k),總結(jié)對(duì)正弦信號(hào)抽樣應(yīng)掌握的原則; 實(shí)驗(yàn) 4 快速 變換(FFT)及其應(yīng)用 一、實(shí)驗(yàn)?zāi)康?1 在理論學(xué)習(xí)的基礎(chǔ)上,通過(guò)本實(shí)驗(yàn),加深對(duì) FFT 的理解,熟悉 FFT 子程序。 2 熟悉應(yīng)用 FFT 對(duì)典型信號(hào)進(jìn)行頻譜分析的方法。 3 了解應(yīng)用 FFT 進(jìn)行信號(hào)頻譜分析過(guò)程中可能出現(xiàn)的問(wèn)題以便在實(shí)際中正確應(yīng)用 FFT。 4 熟悉應(yīng)用 FFT 實(shí)現(xiàn)兩個(gè)序列的線性卷積的方法。 三、實(shí)驗(yàn)內(nèi)容及步驟 實(shí)驗(yàn)中用到的信號(hào)序列: a) 序列 20 b) 衰減正弦序列 c) 三角波序列 d) 反三角波序列 上機(jī)實(shí)驗(yàn)內(nèi)容: (1)
28、、觀察高斯序列的時(shí)域和幅頻特性,固定信號(hào) x a (n)中參數(shù) p=8,改變 q 的值,使 q 分別 等于 2,4,8,觀察它們的時(shí)域和幅頻特性,了解當(dāng) q 取不同值時(shí),對(duì)信號(hào)序列的時(shí)域幅頻 特性的影響;固定 q=8,改變 p,使 p 分別等于 8,13,14,觀察參數(shù) p 變化對(duì)信號(hào)序列的 時(shí)域及幅頻特性的影響,觀察 p 等于多少時(shí),會(huì)發(fā)生明顯的泄漏現(xiàn)象,混疊是否也隨之出 現(xiàn)?記錄實(shí)驗(yàn)中觀察到的現(xiàn)象,繪出相應(yīng)的時(shí)域序列和幅頻特性曲線。 (2)、觀察衰減正弦序列 x b (n)的時(shí)域和幅頻特性,a=0.1,f=0.0625,檢查譜峰出現(xiàn)位置是否 正確,注意頻譜的形狀,繪出幅頻特性曲線,改變 f
29、,使 f分別等于 0.4375 和 0.5625,觀察 21 這兩種情況下,頻譜的形狀和譜峰出現(xiàn)位置,有無(wú)混疊和泄漏現(xiàn)象?說(shuō)明產(chǎn)生現(xiàn)象的原因。 (3)、觀察三角波和反三角波序列的時(shí)域和幅頻特性,用 N=8 點(diǎn) FFT 分析信號(hào)序列 x c (n)和 x d (n)的幅頻特性,觀察兩者的序列形狀和頻譜曲線有什么異同?繪出兩序列及其幅頻特性 曲線。 在 x c (n)和 x d (n)末尾補(bǔ)零,用 N=16點(diǎn) FFT 分析這兩個(gè)信號(hào)的幅頻特性,觀察幅頻特性 發(fā)生了什么變化??jī)汕闆r的 FFT 頻譜還有相同之處嗎?這些變化說(shuō)明了什么? (4)、一個(gè)連續(xù)信號(hào)含兩個(gè)頻率分量,經(jīng)采樣得 x(n)=sin2
30、*0.125n+cos2 *(0.125+ f)n n=0,1,N-1 已知 N=16數(shù)字信號(hào)處理matlab版答案, f分別為 1/16 和 1/64,觀察其頻譜;當(dāng) N=128 時(shí), f不變,其結(jié)果有何不 同,為什么? (5)、用 FFT 分別實(shí)現(xiàn) x a (n)(p8,q2)和 x b (n)(a0.1,f0.0625)的 16 點(diǎn)圓周卷積 和線性卷積。 (6)、產(chǎn)生一 512 點(diǎn)的隨機(jī)序列 x e (n),并用 x c (n)和 x e (n)作線性卷積,觀察卷積前后 x e (n)頻 譜的變化。要求將 x e (n)分成 8 段,分別采用重疊相加法和重疊保留法。 四、實(shí)驗(yàn)思考 1.實(shí)驗(yàn)中的信號(hào)序列 x c (n)和 x d (n),在單位圓上的 Z 變換頻譜|X c ( j )|和|X d ( j )|會(huì)相同嗎?如 果不同,你能說(shuō)出哪一個(gè)低頻分量更多一些嗎?為什么? 2. 對(duì)一個(gè)有限長(zhǎng)序列進(jìn)行 DFT 等價(jià)于將該序列周期延拓后進(jìn)行 DFS 展開,因?yàn)?DFS 也只 是取其中一個(gè)周期來(lái)計(jì)算,所以 FFT 在一定條件下也可以用以分析周期信號(hào)序列。如果實(shí) 正弦信號(hào) sin(2 fn),f=0.1用 16 點(diǎn) FFT 來(lái)做 DFS 運(yùn)算,得到的頻譜是信號(hào)本身的真實(shí)譜嗎?