
使用VAR.P函數和VAR.S函數計算方差方差是在概率論和統計方差衡量隨機變量或一組數據時離散程度的度量,用來度量隨機變量和其數學期望(即均值)之間的偏離程度。Excel 2016中有兩個計算方差的函數,分別是VAR.P函數和VAR.S函數。VAR.P函數計算基于整個樣本總體的方差,基本語法如下。
為必需參數,對應于總體的第一個數值參數。, …為可選參數,對應于總體的2~254個數值參數。VAR.P的計算公式如下。
VAR.S函數估算基于樣本的方差,基本語法如下。

為必需參數,對應于樣本的第一個數值參數。, …為可選參數,對應于樣本的2~254個數值參數。VAR.S的計算公式如下。
公式中的 為樣本平均值, n 為樣本大小。示例15-43 產品包裝質量比較有甲、乙、丙3個車間包裝產品,要求每個產品重量為100g/袋。現在對3個車間隨機各抽取10袋產品進行稱重,稱重數據如圖15-49所示。
在G2單元格中輸入以下公式,并向右復制到I2單元格,計 算各車間包裝產品的平均重量。=(B2:B11)在G3單元格中輸入以下公式,并向右復制到I3單元格,計算各車間包裝產品的偏離程度。=VAR.P(B2:B11)通過對比可以看出,甲、乙車間平均質量均為100g,丙車間超出100g,所以丙車間包裝質量較差。甲車間方差為10.6,乙車間方差為68.2,二者相比,甲車間的方差較小,說明包裝質量更加穩定。使用STDEV.P函數和STDEV.S函數計算標準差標準差在概率統計中常做統計分布程度上的測量,反映組內個體之間的離散程度,平均數相同的兩組數據,標準差未必相同。Excel 2016中有兩個計算標準差的函數,分別是STDEV.P函數和STDEV.S函數。標準差是方差的算術平方根,二者關系如下。

STDEV.P函數計算基于以參數形式給出的整個樣本總體的標準偏差,基本語法如下。
為必需參數標準差公式excel有兩個,對應于總體的第一個數值參數。, …為可選參數,對應于總體的2~254個數值參數。STDEV.P的計算公式如下。
STDEV.S函數基于樣本估算標準偏差,基本語法如下。
為必需參數,對應于樣本的第一個數值參數。, …為可選參數,對應于樣本的2~254個數值參數。STDEV.S的計算公式如下。
公式中的 為樣本平均值標準差公式excel有兩個, n 為樣本大小。示例15-44 某班學生身高分布在圖15-50中,A~B列是某班學生身高記錄表的部分內容,在E1單元格中輸入以下公式計算得到學生的平均身高,結果為177.33(cm)。=(B2:B41)在E2單元格中輸入以下公式,計算學生身高的標準差,返回結果為7.30。=STDEV.P(B2:B41)
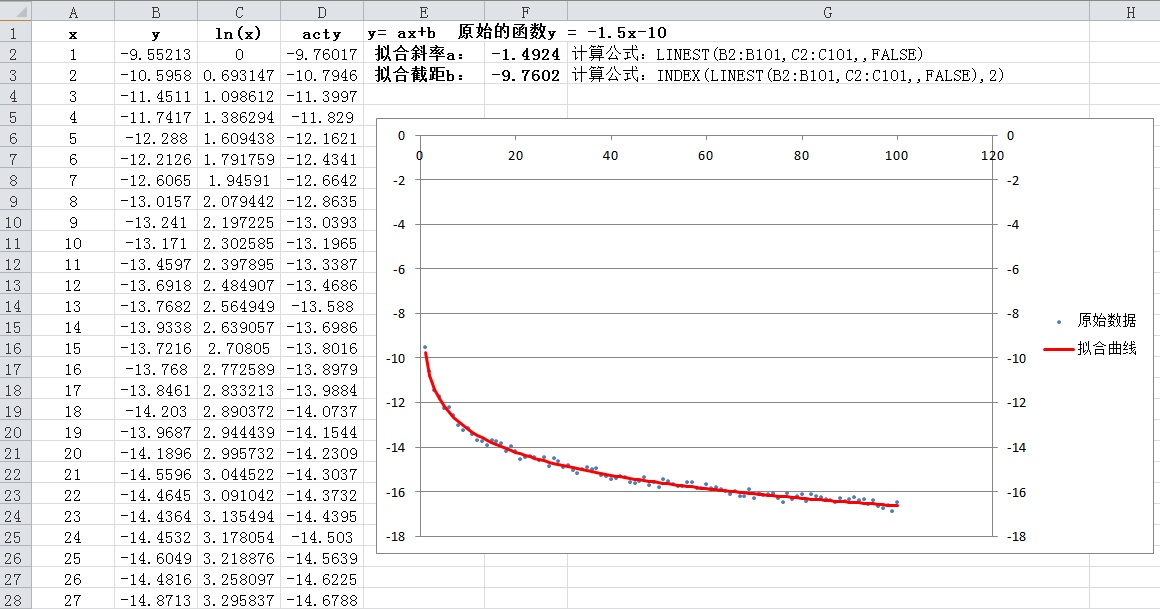
由此可以說明,此班學生的身高主要分布在177.33 ±7.30cm之間。
---------------------------------------------------------------------
推薦圖書
北京大學出版社《Excel 2016函數與公式大全》
▼
1. 專家云集:多位身處各行各業,并身懷絕技的微軟全球有價值專家與您無私分享。多年對 Excel的研究結果進行揭秘。
2. 知識點全覆蓋:詳盡而又系統地介紹了 Excel 2016函數與公式的所有技術特點和應用方法,全面覆蓋相關知識點,完備知識體系無人能及。
3. 解決實際問題:大量源自實際工作的典型案例,通過細致地講解,生動地展示各種應用技巧,快速提高讀者的辦公效率,讓讀者提前完成手頭工作,不用加班。
4. 專業級深度剖析:對常常困擾學習者的功能性特性進行深入剖析,可以讓讀者既能知其然,又能知其所以然。