
描述性統計分析的應用
—基于描述性統計分析識別優質股票
內容導入:
大家好,這里是每天分析一點點。
上期給大家介紹離散趨勢,本期介紹描述性統計分析的基本原理與應用,包括集中趨勢、離散趨勢、偏度與峰度的概念,再結合投資選股案例分析,討論優質股鑒別方法,根據描述性統計指標計算結果解釋原因。文章內容適合數據分析小白,內容深入淺出,案例貼合實際。
下期給大家介紹正態分布的應用,歡迎大家關注。
1
概念介紹:
描述性統計分析的概念:
描述性統計,即概括性度量。是用來概括、表述整體狀況以及事物間關聯、類屬關系的統計方法。通過統計處理可以簡潔地用幾個統計值來表示一組數據的集中性和離散型 (波動性大小)。
數據的頻數分析:
在數據的預處理部分,利用頻數分析和交叉頻數分析可以檢驗異常值。
數據的集中趨勢分析:
用來反映數據的一般水平,常用的指標有平均值、中位數和眾數等。
數據的離散程度分析:
主要是用來反映數據之間的差異程度,常用的指標有方差和標準差。
數據的分布:
在統計分析中,通常要假設樣本所屬總體的分布屬于正態分布,因此需要用偏度和峰度兩個指標來檢查樣本數據是否符合正態分布。
2
描述性統計分析的指標:
分類變量的常用描述指標:
1、頻數:在一組依大小順序排列的測量值中,當按一定的組距將其分組時出現在各組內的測量值的數目,分類變量的頻數即落在各類別中的數據個數。
2、累計頻數:累積頻數就是將各類別的頻數逐級累加起來。
3、百分比:表示一個數是另一個數的百分之幾,也叫百分率或百分數。百分比通常采用符號“%”(百分號)來表示。
4、累積百分比:累積百分比就是將各類別的百分比逐級累加起來。
連續變量的描述分析:
1、絕對數。
2、相對數:倍數、成數、百分數。
3、百分比。
4、百分點:1個百分點=1%,是指變動的幅度。
5、頻數:絕對數,是一組數據中個別數據重復出現的次數。
6、頻率:相對數,次數與總次數的比。。
7、比例:相對數,總體中各部分占全部的比,如:男生的比例是30:50。
8、比率:相對數,不同類別的比,如男女比率是3:2。
9、倍數:相對數,一個數除以另一個數所得的商,如A/B=C,那么A是B的C倍。
10、番數:相對數,指原來數量的2的N次方,如翻一番,意思是原來數量的2倍,翻兩番意思是4倍。
11、同比:相對數,指歷史同時期進行比較,如去年12月與今年12月相比是同比。
12、環比:相對數,指與前一個統計期進行比較,如今年5月與今年4月相比是環比。
描述集中趨勢的指標:
1、均值:數據和值除以數據個數。
2、中位數:數據按照從小到大的順序排列時,最中間的數據即為中位數。
3、眾數:數據中出現次數最多的數字,即頻數最大的數值。
描述離散趨勢的指標:
1、極差:極差=最大值-最小值,是描述數據分散程度的量,且對異常值敏感。
2、四分位數:數據從小到大排列并分成四等份,處于三個分割點位置的數值,即為四分位數。
3、方差和標準差:方差是每個數據值與全體數據的平均數差的平方的平均數。標準差是方差開方。
4、標準分z:對數據進行標準化處理,又叫Z標準化,經過Z標準化處理后的數據符合正態分布。
描述分布形狀的指標:
1、峰度:用來反映頻數分布曲線頂端尖峭或扁平程度的指標。在正態分布情況下,峰度系數值是3(但是SPSS等軟件中將正態分布峰度值定為0,是因為已經減去3,這樣比較起來方便),峰度系數>3,呈現尖峭峰形態,說明觀察量更集中,有比正態分布更短的尾部;峰度系數
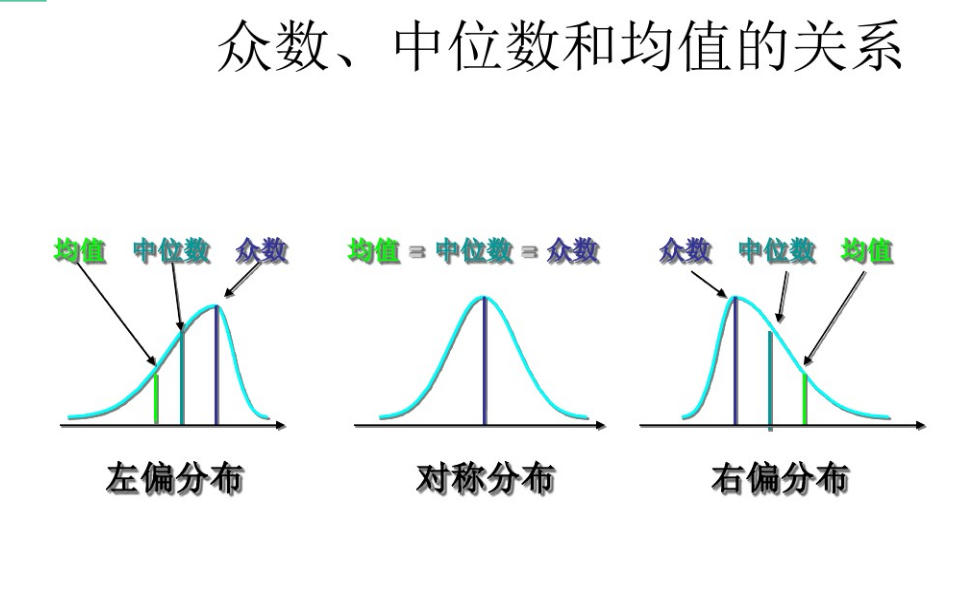
2、偏度:描述分布偏離對稱性程度的一個特征數。當分布左右對稱時,偏度系數為0。當偏度系數大于0時,即重尾在右側時,該分布為右偏。當偏度系數小于0時,即重尾在左側時,該分布左偏。
3
綜合應用場景:
風險投資案例:
# 目前你有500萬資金,準備進行投資,已知有三只股票, 10位專家分別給出了明天的價格預測:
# A股票,現在10元每股,專家的價格預測序列為:
dataA=[11,9,11,11,13,8,14,1,11,11]
# B股票,現在20元每股,專家的價格預測序列為:
dataB=[28,16,20,94,22,24,26,18,17,27]
# C股票,現在50元每股,專家的價格預測序列為:
dataC=[53,59,47,48,58,53,1,128,53,53]
# 你準備現在買股票,明天賣出去,你會選擇那只股票,為什么?
從數據上看,某些專家的預測結果好像不合群,怎么看這些不合群的想法?
題目看似簡單,實則包含套路,不同價格的股票,能買進的數量是不一致的,怎么辦呢?
處理方式非常多:
1、將股票價格“統一”,全部統一為50元或者10元,購買的股票數就是一致的
2、求出利潤率=(股價-股本)/股本 ,相對值就可以一致處理
3、按照當前價格進行計算,處理計算結果
代碼計算過程:
案例選用第三種方式處理,按照當前價格計算后,在對利潤里進行處理。
處理過程如下:
步驟1 股票數據錄入
錄入三支股票預測數據,轉化為series數據格式
import pandas as pd
A股票:
dataA=[11,9,11,11,13,8,14,1,11,11]
A=pd.Series(dataA)
B股票:
dataB=[28,16,20,94,22,24,26,18,17,27]
B=pd.Series(dataB)
C股票:
dataC=[53,59,47,48,58,53,1,128,53,53]
C=pd.Series(dataC)
步驟2剔除異常估計
A股票:
dataA=[11,9,11,11,13,8,14,1,11,11]
A=A.drop(index=7)
#剔除估計中的極小值1
B股票:
dataB=[28,16,20,94,22,24,26,18,17,27]
B=B.drop(index=3)
#剔除估計中的極大值94
C股票:
dataC=[53,59,47,48,58,53,1,128,53,53]
C=C.drop(index=[6,7])
#剔除估計中的極大值與極小值1與128
步驟3計算收入期望
A股票:A=[11,9,11,11,13,8,14,11,11]
a_mean=A.mean()
print('a_mean')
print(a_mean)
B股票:B=[28,16,20,22,24,26,18,17,27]
b_mean=B.mean()
print('b_mean')
print(b_mean)
C股票:C=[53,59,47,48,58,53,53,53]
c_mean=C.mean()
print('c_mean')
print(c_mean)
步驟4計算收入波動
A股票:A=[11,9,11,11,13,8,14,11,11]
a_std=A.std()
print('a_std')
print(a_std)
B股票:B=[28,16,20,22,24,26,18,17,27]
b_std=B.std()
print('b_std')
print(b_std)
C股票:C=[53,59,47,48,58,53,53,53]
c_std=C.std()
print('c_std')
print(c_std)
步驟5計算離散系數
A股票:A=[11,9,11,11,13,8,14,11,11]
print('')
print(a_std/a_mean)
B股票:B=[28,16,20,22,24,26,18,17,27]
print('')
print(b_std/b_mean)
C股票:C=[53,59,47,48,58,53,53,53]
print('')
print(c_std/c_mean)
通過計算,得出的描述性統計分析結果如下表所示:
從利潤率來看,A股票和B股票利潤率都是10%,大于C股票的6%。從風險來看,離散系數,C股票小于A股票小于B股票。
對于期待高收益、能接受較高風險的投資者來說,應該選擇A股票,因為它收益最高,在收益高中的股票中,風險較小。
對于保守的股民來說,應該選擇C股票,雖然收益相對較低,但是安全性好。
對于中等偏下風險的股民來說,可以選擇A股票與C股票的組合策略,既提高了收益,也相對降低了風險。具體如何配比,要看股民能夠承受的風險與期待的利潤。這就是風險分散的魅力。
最后,這個案例不存在選擇B股票的策略,因為他能夠被A股票替代。選B股票的人,有什么理由不選A股票呢。
本期分享到這里,我們會在每周的周三和周五持續更新,咱們下期再見,期待您的光臨。
有什么建議,比如想了解的知識、內容中的問題、想要的資料、下次分享的內容、學習遇到的問題等,請在下方留言。如果喜歡請關注。