
1、將數據在excel 表格中按以下順序排列好。第一列為年份,第二列為省份(省份用1-31個數字表示stata定義面板數據不行,字符不行),后面幾列為變量。
2、將Excel表格另存為CSV格式,在Stata中導入CSV格式的文檔(file--第一個選項,然后點,在跳出的“打開”文檔的文件類型選擇CSV,找到自己之前保存好的CSV文檔)。
3、定義面板數據,輸入以下命令:
. xtset year
4、單位根檢驗
面板數據的單位根檢驗方法有很多種,一般我們只選兩種,即相同根單位根檢驗和不同根單位根檢驗。如果數據是平衡的,則可使用LLC檢驗(適用于同根)和IPS檢驗(適用于不同根)。
一般的stata并沒有自帶這兩個程序需要自己下載安裝,我們可以在命令欄鍵入:, net和 , net,然后按照提示逐步安裝。也可直接輸入命令:ssc ,即自動完成安裝。在開始進行協整檢驗之前,需要將面板數據轉化為時間序列,使用以下命令:tsset year
單位根檢驗輸入如下命令:
變量名,lags(1)
變量名,lags(1)

如果存在單位根,則需要進行一階差分,并再次進行單位根檢驗,輸入以下命令:
D.變量名,lags(1)
注:Users of Stata 11+ use the 。
菜單: > /panel data> Unit-root tests
具體操作可以參照李子奈的說法:單位根檢驗是通過三個模型來完成,首先從含有截距和趨勢項的模型開始,再檢驗只含截距項的模型,最后檢驗二者都不含的模型。并且認為,只有三個模型的檢驗結果都不能拒絕原假設時,我們才認為時間序列是非平穩的,而只要其中有一個模型的檢驗結果拒絕了零假設,就可認為時間序列是平穩的。
例:首先檢驗含有截距和趨勢項的模型:
含有截距和趨勢項的模型存在單位根,再檢驗只含截距項的模型:
所以,lnx不存在單位根,數據是平穩的。
5、協整檢驗
如果基于單位根檢驗的結果發現變量之間是同階單整的,那么我們可以進行協整檢驗。但也有如下的寬限說法:如果變量個數多于兩個stata定義面板數據不行,即解釋變量個數多于一個,被解釋變量的單整階數不能高于任何一個解釋變量的單整階數。另當解釋變量的單整階數高于被解釋變量的單整階數時,則必須至少有兩個解釋變量的單整階數高于被解釋變量的單整階數。如果只含有兩個解釋變量,則兩個變量的單整階數應該相同。
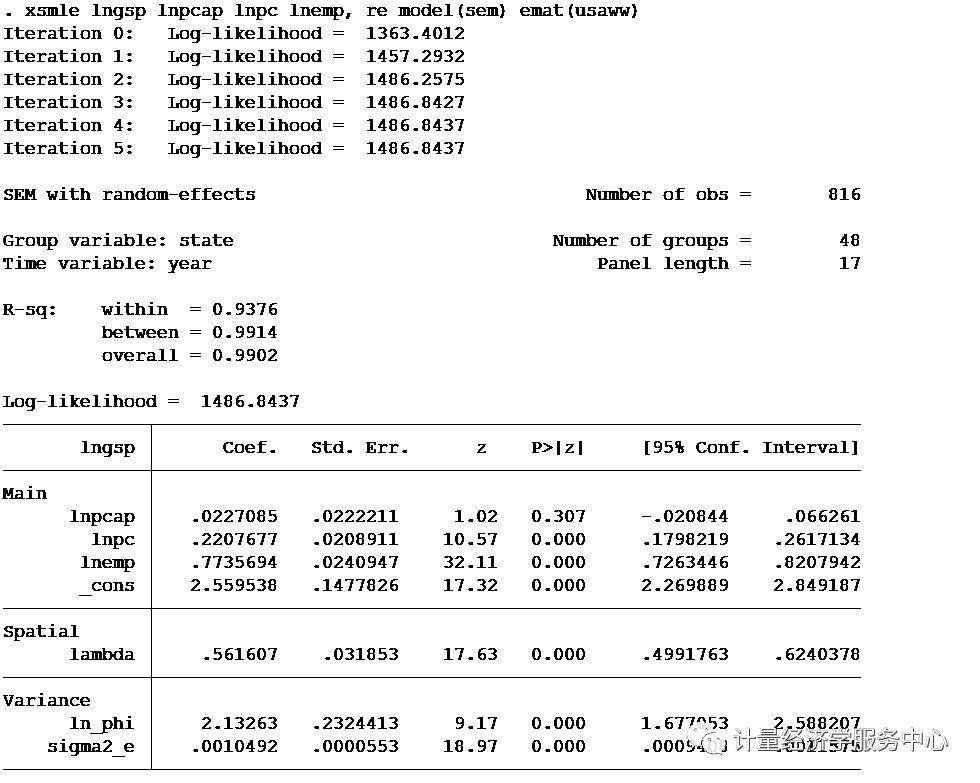
在Stata中對面板數據進行協整檢驗的命令是,這個程序也是需要我們自己下載安裝的。
輸入命令: ,net
然后按提示安裝。也可直接輸入:ssc ,自動完成安裝。
另外一個協整命令:,也是需要安裝的。
在開始進行協整檢驗之前,需要將面板數據轉化為時間序列,使用以下命令:
year
協整的命令為:
[if exp] [in range] , lags(# [#]) leads(# [#])
(#)[ trend (#) mg]
例:

1、 lntfp lnx,lags(1)
2、 , trend lags(1) leads(1) (3)
6、進行回歸分析,輸入以下命令:
Xtreg 因變量 自變量
例如:
固定效應模型的回歸:xtreg lntfp lnx lnxg lnhr lnrd lnfdi,fe
本例中F統計量為0.0000,固定效應非常顯著,表明固定效應模型優于混合OLS模型。
下面,檢驗隨機效應模型是否顯著:
先安裝使用命令:
然后用命令:
檢驗得到的P值為0.0000,隨機效應模型非常顯著,表明隨機效應模型也優于混合OLS模型。至于固定效應模型和隨機效應模型的選擇,則要使用檢驗進行判斷。
7、檢驗判斷選擇固定還是隨機效應模型。檢驗的基本思想是:在固定效應u_i和其他解釋變數不相關的原假設下,用OLS估計的固定效應模型和用GLS估計的隨機效應模型的參數估計都是一致的。反之,OLS是一致的,但GLS則不是。因此,在原假設下,二者的參數估計應該不會有系統的差異,我們可以基于二者參數估計的差異構造統計檢驗量。如果拒絕了原假設,我們就認為選擇固定效應模型是比較合適的。
具體的命令輸入如下:
1. xtreg ,re
2. store
3. xtreg ,fe
4. store fixed
5.
例:
1、. xtreg lntfp lnx lnxg lnfdi,re
2、. store
3、.xtreg lntfp lnx lnxg lnhr lnrd lnfdi,fe
4、. store fixed
5、. fixed
此例中P值為0.0048,拒絕原假設,所以應該選擇固定效應模型。
8、以下是產生新變量以及刪除變量的命令
產生新變量lntfp,將變量tfp轉變為Ln的形式,輸入以下命令:
. gen lntfp=ln(tfp)
刪除變量使用以下命令:
drop 變量名