
翻譯/編輯/部分原創(chuàng) 原作者:Sunil Ray 數(shù)據(jù)圈資深成員
作者簡介:美國達(dá)拉斯一家醫(yī)院數(shù)據(jù)中心工作,職位是data 。主要做方面的數(shù)據(jù)分析建模
在機(jī)器學(xué)習(xí)中,很多時(shí)候你會(huì)掙扎于怎么提高模型的準(zhǔn)確率。在這種時(shí)刻,數(shù)據(jù)探索的一些方法將幫助你解決這個(gè)問題。這個(gè)指導(dǎo)將幫助你理解數(shù)據(jù)探索中的主要技術(shù)。請記住你輸入的變量的數(shù)據(jù)質(zhì)量決定了你模型輸出量的質(zhì)量。所以當(dāng)你的商業(yè)問題提出來以后,你需要花費(fèi)很多時(shí)間在數(shù)據(jù)準(zhǔn)備和探究上面,一般來說,數(shù)據(jù)清理,探究和準(zhǔn)備大概占據(jù)了一個(gè)項(xiàng)目70%的時(shí)間。下面是準(zhǔn)備,理解,清理你用于建立預(yù)測模型的數(shù)據(jù)的幾個(gè)步驟,我會(huì)一個(gè)一個(gè)來介紹
1.變量確定
2.單變量分析
3.雙變量分析
4.處理缺失值
5.處理離群值
6.變量轉(zhuǎn)換
7.變量創(chuàng)建
首先上部會(huì)介紹1,2,3,4四個(gè)部分。
變量確定
首先,你需要確認(rèn)你的輸入變量(預(yù)測指標(biāo))和你的輸出變量(目標(biāo)變量)是什么,接著,你需要確認(rèn)數(shù)據(jù)的種類和分類。下面用一個(gè)簡單的例子來說明,假設(shè)現(xiàn)在我們想要預(yù)測學(xué)生是否玩板球(),現(xiàn)在我們需要確定輸入變量,輸出目標(biāo)變量,以及每一個(gè)變量的分類和種類,下面是部分原數(shù)據(jù)
:學(xué)生編號
:性別(F-女,M-男)
:之前的考試分?jǐn)?shù)
(cm):身高(厘米)
(kgs):體重(千克)
Play :玩板球(1:玩板球,0:不玩板球)
下面這個(gè)圖是以上變量的分類和種類圖
從上圖可以看到,輸入變量(預(yù)測變量)是性別,之前的考試分?jǐn)?shù),身高,體重。而輸出值(目標(biāo)變量)是是否玩板球。學(xué)生編號和性別是字符變量(),是否玩板球,之前的考試分?jǐn)?shù),身高,體重是數(shù)字變量()。從連續(xù)和非連續(xù)來分類的話,性別和是否玩板球是非連續(xù)變量(),之前考試的分?jǐn)?shù),身高和體重是連續(xù)變量()
單變量分析
在這個(gè)步驟,我們需要一個(gè)變量一個(gè)變量的去做分析,單變量分析的方法取決于你需要分析的變量是連續(xù)的還是非連續(xù)的。

連續(xù)型變量( ):對于連續(xù)型變量我們需要知道這個(gè)變量的中心( )和展布( or ),下面是描述變量中心還有展布的指標(biāo)量,以及用什么圖來進(jìn)行可視化。
中心:平均值,中位數(shù),眾數(shù),最小值,最大值
展布分布:范圍,四分位數(shù),內(nèi)距(四分位距),方差,標(biāo)準(zhǔn)差,偏態(tài)與峰度
可視化方法:直方圖(最右的圖),箱線圖(中間一個(gè)圖)
非連續(xù)型變量( ):對于非連續(xù)型變量,我們使用頻率表來顯示每一個(gè)分類的分布,同時(shí)我們也可以計(jì)算每一個(gè)分類的百分比。一般可以使用條形圖或者箱線圖來可視化
雙變量分析
雙變量分析是用來找出兩個(gè)變量之間的關(guān)系,我們尋找兩個(gè)變量間有顯著水平的相關(guān)聯(lián)和非相關(guān)聯(lián)性。雙變量分析可以是非連續(xù)型變量和非連續(xù)型變量,非連續(xù)型變量和連續(xù)型變量還有連續(xù)型變量和連續(xù)型變量。下面我們將一個(gè)一個(gè)情形來說明。
連續(xù)型變量和連續(xù)型變量:對于兩個(gè)連續(xù)型變量,一般可視化我們使用散點(diǎn)圖。散點(diǎn)圖很好的顯示了兩個(gè)變量的關(guān)系,這個(gè)關(guān)系可以是線性也可以是非線性的。
上面的六個(gè)圖,左上是很強(qiáng)的正相關(guān),意思是指當(dāng)其中一個(gè)變量增加時(shí),另外一個(gè)變量增加,上面正中間的是中等強(qiáng)的正相關(guān),右上是沒有相關(guān)性,左下是中等強(qiáng)的負(fù)相關(guān),意思是指當(dāng)其中一個(gè)變量增加時(shí),另外一個(gè)變量減少,下面正中間是很強(qiáng)的負(fù)相關(guān),右下是非線性的相關(guān)。一般散點(diǎn)圖只是顯示了兩連續(xù)變量之間的關(guān)系,但是并沒有顯示關(guān)系的強(qiáng)度大小。所以我們使用一個(gè)指標(biāo)相關(guān)()來顯示關(guān)系強(qiáng)度的大小,相關(guān)的大小可以從-1到+1。其中“-1”指的是完美的負(fù)線性相關(guān),“+1”指的是完美的正線性相關(guān),“0”指的是沒有線性相關(guān)(但是可能有非線性的關(guān)系)。計(jì)算相關(guān)的公式如下
相關(guān)=變量X和Y的協(xié)方差/變量X的方差和變量Y的方差乘積的平方根
如果使用Excel,可以用()來計(jì)算兩個(gè)變量的相關(guān)。如果使用SAS可以使用PROC CORR來計(jì)算相關(guān),如果用R,可以使用cor.test()來計(jì)算相關(guān)。如果用,可以使用numpy.()來計(jì)算。下面是用EXCEL計(jì)算相關(guān)的例子,X和Y的相關(guān)系數(shù)是0.65。
非連續(xù)變量和非連續(xù)型變量:
雙向表(two-way table):我們可以用一個(gè)雙向表來分析兩個(gè)非連續(xù)變量的關(guān)系,雙向表的行代表一個(gè)非線性變量的分類,列代表另一個(gè)非線性變量的分量,然后每個(gè)小格(cell)可以顯示數(shù)目還有所占的百分比(雙向表是下面最左邊的表)。
堆積柱圖( Chart):這個(gè)其實(shí)就是雙向表的可視化(上面右邊兩個(gè)表)
卡方檢驗(yàn)(Chi- Test):這個(gè)檢驗(yàn)是用來檢驗(yàn)變量關(guān)系的顯著性。主要是比較兩個(gè)及兩個(gè)以上樣本率( 構(gòu)成比)以及兩個(gè)分類變量的關(guān)聯(lián)性分析。其根本思想就是在于比較理論頻數(shù)和實(shí)際頻數(shù)的吻合程度或擬合優(yōu)度問題。它會(huì)反饋用卡方分布計(jì)算的p值,當(dāng)p=0的時(shí)候,這兩個(gè)變量是相互依賴的(),當(dāng)p=1的時(shí)候,可以理解為這兩個(gè)變量獨(dú)立(),當(dāng)p值小于0.05的時(shí)候,意味著有95%的信心這兩個(gè)變量的依賴性是顯著的。卡方檢驗(yàn)的統(tǒng)計(jì)量是
其中O表示實(shí)際觀察到的頻數(shù),而E表示當(dāng)這兩個(gè)變量獨(dú)立的時(shí)候,雙向表中每個(gè)cell的理論頻數(shù)。
非連續(xù)變量和連續(xù)型變量:
對于探索連續(xù)變量和非連續(xù)變量的關(guān)系,對于可視化,我們可以畫非連續(xù)變量每一個(gè)分類的箱線圖()。而如果想用統(tǒng)計(jì)方法來檢驗(yàn)它們之間的關(guān)系是否顯著,可以使用Z檢驗(yàn),t檢驗(yàn)或者方差分析(ANOVA)。一般Z檢驗(yàn)用于樣本比較大的情況,檢驗(yàn)的是兩組之間的均值是否有顯著不同。t檢驗(yàn)一般用于樣本比較小的情況(每一組都小于30),檢驗(yàn)的也是兩組之間均值是否有顯著不同。而ANOVA是用來檢驗(yàn)多于兩組的時(shí)候, 多個(gè)組的均值是否有不同。
缺失值處理
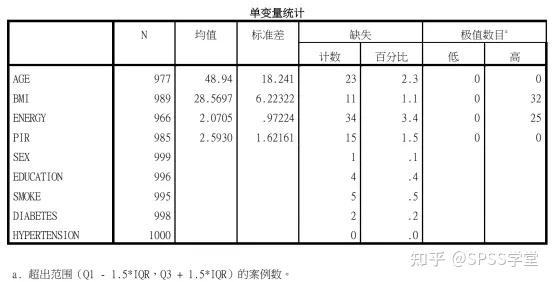
在數(shù)據(jù)清理中,我們經(jīng)常會(huì)遇到很差的數(shù)據(jù),會(huì)有很多缺失值,如果訓(xùn)練數(shù)據(jù)中有缺失值的話會(huì)讓訓(xùn)練出來的模型有偏差或者不夠擬合數(shù)據(jù)。缺失值出現(xiàn)的原因也有很多種,它們一般出現(xiàn)在兩個(gè)階段
數(shù)據(jù)抓取:在抓取數(shù)據(jù)過程中,因?yàn)闆]有符合抓取的指導(dǎo)或者要求,而造成的一種缺失,這種缺失比較容易被發(fā)現(xiàn)并且很快的改正
數(shù)據(jù)收集:在數(shù)據(jù)收集階段的缺失比較難改正,因?yàn)橛写蟾潘姆N不同的情況
完全隨機(jī)缺失( at ):這種情況是指對每一個(gè)觀測值,缺失的概率是一樣的。打個(gè)比方,比如現(xiàn)在需要一群人上報(bào)自己的收入,對于每一個(gè)上報(bào)者,在上報(bào)之前先丟硬幣,如果是正面就上報(bào)收入,如果是反面就隱瞞收入。因此對每個(gè)觀測值都有一半的機(jī)會(huì)缺失或者不缺失。
隨機(jī)缺失( at ):隨機(jī)缺失是指缺失值是任意缺失的但是對不同的輸入變量和分組分類變量和連續(xù)變量怎么做散點(diǎn)圖,缺失值的比例是不同的。比如當(dāng)我們想收集女性的年齡時(shí),女性比起男性會(huì)有更多的缺失值(很好理解,女性一般不太喜歡被訪問年齡)。
缺失依賴于未觀測到的自變量 ( that on ):
當(dāng)缺失值不是任意隨機(jī)的,而是和某些我們沒有觀測到的值有關(guān)。打個(gè)比方,比如在醫(yī)藥研究中,如果一種治療方法引起了病人身體的不適應(yīng),那么病人有很大的概率會(huì)提前從這個(gè)研究中退出導(dǎo)致最后他/她的觀測值是缺失的,這種缺失不是任意的而是和身體不適應(yīng)相關(guān)的。
缺失值依賴于缺失值本身 ( that o the value ):
當(dāng)缺失的概率直接和缺失值本身有關(guān)的時(shí)候。比如,一般很高收入和很低收入的人不太喜歡被訪問收入多少,因此收入會(huì)有缺失值。
處理缺失值的方法
a. 刪除:表刪除(List-wise )和對刪除(Pair-wise)
通常的數(shù)據(jù)表中,行代表樣本,列代表不同的變量。在列表刪除中,只要一行有任何一個(gè)變量的值有缺失,我們就刪除一整行的信息。簡單是這個(gè)方法的主要優(yōu)勢,但是很大的劣勢也是這樣嚴(yán)格的刪除會(huì)導(dǎo)致樣本量的減少。在成對刪除中,我們對每一個(gè)變量就用它不缺失的樣本數(shù)進(jìn)行逐個(gè)分析,這種方法盡量的保留了樣本個(gè)數(shù),但是不好的是對每一個(gè)變量你所使用的樣本個(gè)數(shù)也不一樣。兩種刪除方法如下圖例子所示,左邊是表刪除,而右邊是對刪除,你可以看到左下圖任何一行有缺失就會(huì)被劃掉刪除,而右下表,對性別(),勞動(dòng)力(),銷售(sales)變量每一個(gè)分別刪除缺失值,而不是一行全部劃掉。
主要備注:刪除的方法只能用于完全隨機(jī)缺失( at )的情況,隨意刪除不隨機(jī)的缺失值會(huì)使數(shù)據(jù)產(chǎn)生bias。
b. 均值(mean)/眾數(shù)(mode)/中位數(shù)()替換法
替換法是用估計(jì)的值去替換缺失值的方法。這個(gè)方法的目的是利用已知的可以定義的不缺失的數(shù)據(jù)去幫助估計(jì)缺失的數(shù)據(jù)。均值/眾數(shù)/中位數(shù)這三個(gè)都是經(jīng)常被廣泛使用的方法。這種替換法一般也有兩大類:
第一種就是一半的替換,就是我們計(jì)算缺失的變量剩下不缺失的數(shù)據(jù)的均值,眾數(shù)或者中位數(shù)來替換缺失值。例如上圖那個(gè)例子,對勞動(dòng)力那一個(gè)變量的缺失值,我們計(jì)算不缺失的勞動(dòng)力的數(shù)據(jù)得到28.33,然后用這個(gè)值來替換缺失值。
第二種就是相似替換,比如在上圖那個(gè)例子里的勞動(dòng)力,我們分別計(jì)算不缺失的男和女的勞動(dòng)力平均值,分別是男29.75而女25,因此對于男,缺失的勞動(dòng)力就用29.5替代,而對于女,缺失的勞動(dòng)力就用25替代。
c.預(yù)測模型
用預(yù)測模型來估算缺失值也是一種理論比較成熟的方法。一般我們會(huì)把數(shù)據(jù)集分為兩個(gè)部分,一個(gè)部分完全沒有缺失值,而另一個(gè)部分含有缺失值。沒有缺失值的數(shù)據(jù)集作為我們的訓(xùn)練數(shù)據(jù)集來得到預(yù)測模型,而有缺失值的數(shù)據(jù)集作為檢驗(yàn)數(shù)據(jù)集,而缺失的變量就作為要預(yù)測的目標(biāo)輸出量。下一步,我們用訓(xùn)練集生成一個(gè)預(yù)測模型,用其他的變量來預(yù)測缺失的變量,然后把預(yù)測模型用到檢驗(yàn)數(shù)據(jù)集來得到缺失部分的預(yù)測值。我們可以使用回歸,方差分析,邏輯回歸或者其他的機(jī)器學(xué)習(xí)的方法去做預(yù)測模型。
不過這個(gè)方法也有明顯的缺點(diǎn),如果缺失的變量與其他的變量沒有什么關(guān)系,這個(gè)預(yù)測將會(huì)不準(zhǔn)確。
d. 最近鄰居法(KNN)
在這個(gè)替換方法中,我們用缺失值周圍的離它最近或者是最相似的其他變量來估算。一般兩個(gè)變量的相似度是有距離來決定的。距離的定義可以有多種。這個(gè)方法的優(yōu)點(diǎn)就是缺失值是連續(xù)的或者非連續(xù)的變量都可以替換。不需要對每一個(gè)缺失的變量生成預(yù)測模型。數(shù)據(jù)變量間的關(guān)系也都被考慮進(jìn)去了。而缺點(diǎn)是對于很大的數(shù)據(jù)集,這個(gè)方法很耗時(shí),因?yàn)樗鼤?huì)搜索所有的相似變量,而且k值的選擇(就是缺失值周圍選k個(gè)點(diǎn))也是很重要的,高的k值會(huì)讓幾乎和缺失變量不相關(guān)的變量包含進(jìn)來,而低的k值都會(huì)把很相關(guān)的變量可能排除出去。
在機(jī)器學(xué)習(xí)中,很多時(shí)候你會(huì)掙扎于怎么提高模型的準(zhǔn)確率。在這種時(shí)刻,數(shù)據(jù)探索的一些方法將幫助你解決這個(gè)問題。這個(gè)指導(dǎo)將幫助你理解數(shù)據(jù)探索中的主要技術(shù)。請記住你輸入的變量的數(shù)據(jù)質(zhì)量決定了你模型輸出量的質(zhì)量。所以當(dāng)你的商業(yè)問題提出來以后,你需要花費(fèi)很多時(shí)間在數(shù)據(jù)準(zhǔn)備和探究上面,一般來說,數(shù)據(jù)清理,探究和準(zhǔn)備大概占據(jù)了一個(gè)項(xiàng)目70%的時(shí)間。下面是準(zhǔn)備,理解,清理你用于建立預(yù)測模型的數(shù)據(jù)的幾個(gè)步驟,我會(huì)一個(gè)一個(gè)來介紹
1.變量確定
2.單變量分析

3.雙變量分析
4.處理缺失值
5.處理離群值
6.變量轉(zhuǎn)換
7.變量創(chuàng)建
在下部會(huì)介紹5,6,7三個(gè)部分。
處理離群值
離群值()經(jīng)常會(huì)引起很多錯(cuò)誤的模型估算和預(yù)測。簡單的講,離群值就是離整體數(shù)據(jù)分布或者模式很遠(yuǎn)的觀測點(diǎn)。舉個(gè)簡單的例子,一個(gè)研究顯示一般人的年收入是8萬,但是發(fā)現(xiàn)其中有兩個(gè)用戶的年收入有4塊錢或者400百萬,這兩個(gè)用戶就可以看成是離群點(diǎn)。下圖就是一個(gè)箱線圖的離群點(diǎn)的例子,被圈出來的就是離群點(diǎn)。
離群值的種類
離群值一般有兩個(gè)種類,一個(gè)是一元離群值,一個(gè)是多元的離群值。比如上面箱線圖的離群值點(diǎn)。這種離群值一般是在我們觀察單變量的分布的時(shí)候。 而多元離群值是指多維的空間,如果想找到他們,你必須看數(shù)據(jù)點(diǎn)的多維分布。讓我們用身高和體重之間的關(guān)系來理解一元和多元離群值。如下圖,左下和左中分別是身高和體重分別的箱線圖,我們并沒有看到離群值,而當(dāng)我們畫出右下圖的身高體重散點(diǎn)圖的時(shí)候,我們發(fā)現(xiàn)了三個(gè)離群值。
知道了離群值的分類,每次當(dāng)我們遇到離群值的時(shí)候,最好的辦法就是找到為什么這些值會(huì)離群。離群值產(chǎn)生的原因也可以分為兩大類
假的離群(就是誤差)/非自然的離群:
1.輸入誤差:就是在數(shù)據(jù)收集中產(chǎn)生的人為的錯(cuò)誤,比如數(shù)據(jù)記錄,數(shù)據(jù)輸入錯(cuò)誤都會(huì)引起離群值。打個(gè)比方,一個(gè)顧客的年收入有十萬元,而數(shù)據(jù)輸入員將它輸入成了100萬元,是原來的十倍。這個(gè)就會(huì)造成離群點(diǎn)。
2.測量誤差:這是最常見的離群值的來源,這個(gè)一般是由測量儀器的錯(cuò)誤造成的。比如,你有十個(gè)測量儀器,其中9個(gè)是準(zhǔn)確的一個(gè)是壞的。那么被壞儀器測量的組將會(huì)比其他儀器測量的組高或者低一些。這樣會(huì)引起離群點(diǎn)。
3.故意的離群值:這個(gè)經(jīng)常發(fā)生在一些有敏感數(shù)據(jù)的自我報(bào)告中。打個(gè)比方,比如青少年一般會(huì)少報(bào)他們一周喝酒的數(shù)量分類變量和連續(xù)變量怎么做散點(diǎn)圖,只有很少的一部分青少年會(huì)如實(shí)匯報(bào)。那么因?yàn)榇蟛糠秩硕忌賵?bào),那實(shí)際匯報(bào)的那些數(shù)據(jù)反而看起來像離群點(diǎn)了。
4. 數(shù)據(jù)處理誤差:當(dāng)我們做數(shù)據(jù)分析的時(shí)候,我們會(huì)從不同的平臺(tái)抓取數(shù)據(jù),那么這些抓取和轉(zhuǎn)換回來帶一些誤差,從而產(chǎn)生離群值。
5. 樣本誤差:很簡單的比方,比如我們要測量一般運(yùn)動(dòng)員的身高,但是我們不小心把幾個(gè)籃球隊(duì)員算進(jìn)去了,因此這些造成了離群值。
自然離群
當(dāng)一個(gè)離群值不是因?yàn)檎`差引起的,那么就是自然離群值,比如,有時(shí)候在比賽中,前面五十名比后面的幾百個(gè)人好太多,那一般不是因?yàn)檎`差,因?yàn)殡x群值很多,那這種情況,就屬于自然離群,我們需要單獨(dú)對待這一部分人。
離群值的影響
離群值會(huì)很明顯的改變數(shù)據(jù)分析與建模的結(jié)果,他們有很多的不好的影響
1.它們會(huì)增加誤差的方差,而一般誤差的方差平方根會(huì)作為統(tǒng)計(jì)量的分母,因?yàn)闇p小統(tǒng)計(jì)量的大小,造成p值變大,從而降低模型的統(tǒng)計(jì)功效。
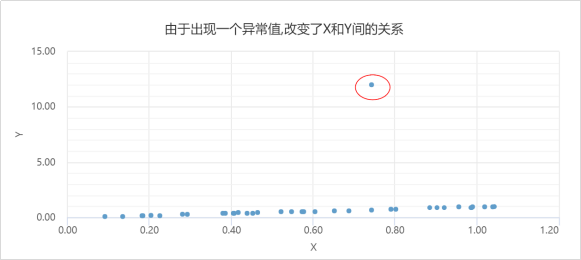
2.如果離群值是非隨機(jī)分布的,那么它們會(huì)影響數(shù)據(jù)正態(tài)性分布。而很多線性模型的假設(shè)就是輸出變量Y是正態(tài)分布。
3.離群值還會(huì)影響估計(jì)值,讓其差生偏差
4.離群值也會(huì)影響很多統(tǒng)計(jì)方法的統(tǒng)計(jì)假設(shè)比如線性回歸,方差分析。
為了容易理解,我們看一個(gè)簡單的例子,如下圖
在右上圖,因?yàn)橛辛穗x群值300,而導(dǎo)致標(biāo)準(zhǔn)差,均值什么的都產(chǎn)生了很大變化。這會(huì)完全改變你的統(tǒng)計(jì)估計(jì)。
離檢驗(yàn)離群值
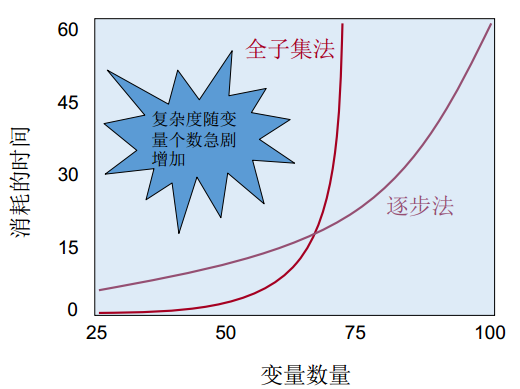
絕大多數(shù)探測離群值的方法都是可視化數(shù)據(jù),我們使用不同的可視化方法,比如箱線圖,頻率圖,散點(diǎn)圖。當(dāng)然也有一些簡單判斷的準(zhǔn)則。比如對于一元離群值,對于任意的數(shù)據(jù),一般的范圍是正負(fù)1.5倍的四分衛(wèi)距(IQR)這種。而二元或多元離群值一般是用一種距離計(jì)算來判斷,比如馬氏距離或者線性回歸中的Cook距離。
移除離群值
絕大多數(shù)處理離群值的方法與缺失值比較類似,可以刪除或者轉(zhuǎn)換,或者替換。
刪除觀測值: 如果是因?yàn)榉亲匀坏碾x群值,而且數(shù)量很少的話,我們可以移除它們。
轉(zhuǎn)換以及給變量分組:轉(zhuǎn)換變量可以減少離群值,比如給變量取自然對數(shù)。然后對變量進(jìn)行分組也是個(gè)不錯(cuò)的轉(zhuǎn)換方法。比如對于分組過的變量,決策樹就可以很好地處理這些離群值。而且我們還可以給不同的觀測值不同的權(quán)重。比如下圖右邊就是把左邊的觀測值進(jìn)行了取自然對數(shù)過后得到的新觀測值。
替換: 類似于缺失值的替換,我們也可以替換離群值,可以使用均值,中位數(shù),眾數(shù)等方法。如果是非自然的離群值,我們可以用統(tǒng)計(jì)方法去預(yù)測離群值。
單獨(dú)處理:與缺失值處理不同以及增加的一項(xiàng),就是單獨(dú)處理了。如果離群值數(shù)量很多,我們在統(tǒng)計(jì)建模中,應(yīng)該把它們單獨(dú)作為一組單獨(dú)分析。一般來說比較流行的統(tǒng)計(jì)方法,有那種對不同的組分別建模然后給權(quán)重進(jìn)行聯(lián)合的方法。
變量變換
現(xiàn)在讓我們跳到數(shù)據(jù)探索的最后一個(gè)階段:特征工程。在介紹6.變量變換和7.變量創(chuàng)建時(shí),先介紹一下特征工程,因?yàn)?和7是特征工程很重要的組成部分。特征工程是建模中很重要的一步,是怎么從已有的數(shù)據(jù)中提取更有用信息的藝術(shù)。你并不添加任何數(shù)據(jù),而是讓你現(xiàn)有的數(shù)據(jù)怎么變得更加有用。一般特征工程的前五步就是我之前介紹的1,2,3,4,5.而后面兩步就是變量變換和變量創(chuàng)建。這兩步對你模型的預(yù)測準(zhǔn)確度有很大的影響。
在數(shù)據(jù)建模中,變量變換是指一個(gè)變量用其相關(guān)的函數(shù)變換之后的值來表示。打個(gè)比方,我們用x取對數(shù)之后的值來取代x的值。也可以說,變量變換改變了變量的分布。那什么時(shí)候我們需要使用變量變換呢。下面是四種情況:
1.當(dāng)我們想要改變一個(gè)變量的scale活著標(biāo)準(zhǔn)化它想讓這個(gè)變量的變得更容易理解。如果你的數(shù)據(jù)有不同的,這種改變并不改變變量的分布的形狀
2.當(dāng)我們想要把變量之間非線性的關(guān)系變成線性的。一般來講,線性關(guān)系比非線性的關(guān)系容易讓人理解。變量變量可以幫助我們完成這個(gè)。一般散點(diǎn)圖可以讓我們可視化兩個(gè)連續(xù)變量之間的關(guān)系。比如取對數(shù)變換是我們經(jīng)常用的方法。
3. 比起傾斜分布的變量,我們更喜歡對稱分布的變量。對稱分布的變量比較容易解釋而且也易于用于參數(shù)估計(jì)。比如一般線性回歸會(huì)要求誤差服從正態(tài)分布,這里的正太分布就是對稱分布的一種。對于參數(shù)模型,我們一般都有變量的分布假設(shè),而很多時(shí)候,我們都假設(shè)變量是對稱分布,模型的理論推導(dǎo)也是建于對稱分布而來的。因此每當(dāng)你有遇到很傾斜的分布的時(shí)候,最好對變量做一些變換。比如,對于向右傾斜的分布,我們可以去平方根或者立方根,也可以去對數(shù)。而對于向左傾斜的分布,我們可以平方,或者立方或者指數(shù)化我們的變量。比如右下圖向右傾斜的分布我們就指數(shù)化我們的變量
4. 有時(shí)候變量變換是來自于項(xiàng)目的要求,或者說能更好的完成項(xiàng)目的任務(wù)。打個(gè)比方,在某個(gè)人力資源的分析中,我們發(fā)現(xiàn),年齡和員工的表現(xiàn)有很大的關(guān)系。年齡越大,表現(xiàn)越好。從應(yīng)用的觀點(diǎn)來看,一般更喜歡把年齡分層成比如45歲,然后對每一組年齡層,采用不同的策略。這種方法就叫做變量分層()
知道什么時(shí)候做變量變換了,那有哪些變量變換的基本方法呢
取對數(shù):一般用于向右傾斜分布的變量,但是它不能用于0或者負(fù)值
平方根/立方根:平方根或者立方根變量也可以改變變量分布,不過不如取對數(shù)明顯。但是立方根有自己的優(yōu)勢,它可以用于0值還有負(fù)值。平方根變量可以用于含0的正值。
分組():這個(gè)適用于分組變量,很多時(shí)候這種分組是建立于商業(yè)理解上。比如我們會(huì)把收入分為高收入,中等收入和低收入。當(dāng)然我們有兩個(gè)變量還可以一起做多元分組。
變量建立
變量建立是利用原有的變量創(chuàng)建新變量的過程。打個(gè)比方,我們有日期的輸入變量(日-月-年),我們可以利用這個(gè)變量建立專門的日,月,年,星期,工作日等等比之前的輸入變量日期更好的變量。這個(gè)方法有時(shí)候用來強(qiáng)調(diào)變量的一些隱藏信息和關(guān)系。下面這個(gè)表就是把日期(date)變成三個(gè)新的變量(,,)的例子。
當(dāng)然創(chuàng)建變量有很多方法,下面就介紹其中的兩種:
創(chuàng)建派生的變量:
這個(gè)是從原有的變量中通過函數(shù)或者其他的方法得到新的派生變量。比如競賽中很有名的泰坦尼克號數(shù)據(jù),很多參賽者會(huì)喜歡從人的名字變量中創(chuàng)建,Mr,Mrs和Miss這四個(gè)新變量。那一般怎么決定派生變量呢。大部分時(shí)候要按你的商業(yè)要求來。
創(chuàng)建虛擬的變量:
還有一個(gè)普遍的情況就是創(chuàng)建所謂的虛擬變量,一般用虛擬變量把非線性的變量變成數(shù)值變量。虛擬變量又叫指標(biāo)變量。比如對于性別()有男和女兩種,那么我們可以建立兩個(gè)新的變量一個(gè)叫,它的值為 1(男)和0(女),然后變量,它的值為 0(男)和1(女)。如果非連續(xù)變量有n層(大于2),那么可以創(chuàng)建n-1個(gè)虛擬變量。下面這個(gè)圖就是用性別變量()來創(chuàng)建兩個(gè)虛擬變量(dummy )。
數(shù)據(jù)探索就介紹完了。總之,任何時(shí)候都不要小看data ,它是你建立模型的第一步。
關(guān)注我就是關(guān)注你的未來,后續(xù)還有系列文章
目前已有550+位行業(yè)人士加入.......
歡迎加入數(shù)據(jù)君數(shù)據(jù)分析秘密組織(收費(fèi))
(保存圖到手機(jī)相冊,然后微信掃,才可以加入)
這是一份事業(yè)!
數(shù)據(jù)挖掘與大數(shù)據(jù)分析
()
傳播數(shù)據(jù)|解讀行業(yè)|技術(shù)前沿|案例分享
2013年新浪百強(qiáng)自媒體
2016年中國十大大數(shù)據(jù)影響平臺(tái)
榮譽(yù)不重要,干貨最實(shí)在