
前言
最短路徑問題是圖論研究中的一個經典算法問題,圖中從一個頂點到達另一個頂點的路徑可能不止一條,最短路徑問題旨在尋找圖(由結點和路徑組成的)中兩結點之間的最短路徑。本文討論兩種常見的最短路徑問題--單源最短路徑問題和多源最短路徑問題。
一、單源最短路徑
單源最短路徑是指從從一個固定的起始點出發到其余所有點的路徑。在單源最短路徑中,根據是否存在負權邊對相應的算法進行了更為細致的分類。
1.1權值均為正的單源最短路徑
給定一個帶權有向圖 D 與源點 v ,求從v 到 D 中其它頂點的最短路徑。限定各邊上的權值大于0。
如何求得這些路徑?迪杰斯特拉()提出了一個按路徑長度遞增的次序產生最短路徑的算法。首先求出長度最短的一條最短路徑,再參照它求出長度次短的一條最短路徑,依次類推,直到從頂點 v 到其它各頂點的最短路徑全部求出為止。
解決步驟描述:
1. 設置輔助數組dist。它的每一個分量dist[i]表示當前找到的從源點 v0到終點 vi的最短路徑的長度;
2. 初始狀態:
2.1. 若從源點 v1到頂點 vi有邊:dist[i]為該邊上的權值;
2.2. 若從源點 v1到頂點 vi無邊:dist[i]為∞。
根據以上描述,可以得到如下描述的算法:
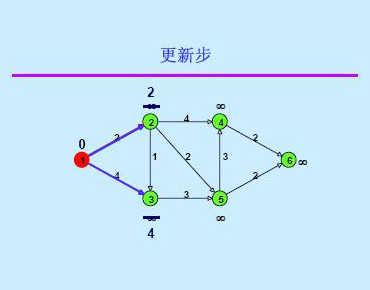
1,將集合S初始化為{V1},易知dist[2]=10,dist[3]=∞,dist[4]=∞,dist[5]=5。則第一輪選出的最小的dist[5],將5放入集合S
2,因為有了頂點5的加入,需要更新dist數組。易知idst[2]=8,dist[3]=14,dist[4]=7;則在第二輪選出最小的dist[4],將4放入集合S
3,依此類推......直到全部的頂點包含在集合S中。
代碼示例:
void Dijkstra(int sv) //起點sv
{
int i = 0;
int j = 0;
// 合法性判斷
if( (0 <= sv) && (sv < VNUM) ) //VNUM頂點個數
{
// 初始化輔助數組
for(i=0; i int index = -1; // 下個最短路徑的頂點
// 遍歷其余未被標記的頂點,找到最短路徑及最短路徑的頂點
for(j=0; j
int index = -1; // 下個最短路徑的頂點
// 遍歷其余未被標記的頂點,找到最短路徑及最短路徑的頂點
for(j=0; j -1 )
{
Mark[index] = 1;
}
// 更新當前最短路徑及頂點
for(j=0; j %d: %d\n", sv, p, Dist[p]);
// 最短路徑頂點關系
do
{
printf("%d <- ", p);
p = P[p];
} while( p != sv );
printf("%d\n", p);
}
}
? 1.2權值有負的單源最短路徑
當一張圖中存在負權邊時,算法就無法算出正確的解,這個時候我們要用到-Ford算法[6]。但是,需要注意:1,當這張圖存在負權環時是無法算出最短路徑的,不過也可以用-Ford算法判斷這張圖是否有負權環。2,-Ford算法一般處理的是有向圖,因為如果是無向圖,那么如果存在一條負權邊,就會構成負權環了。
算法原理:
如果一個圖沒有負權環,那么從一點到另一個點的最短路徑最多經過所有的V個頂點,經過V-1條邊。對一個點的一次松弛操作前k條最短路徑算法,就是找到經過這個點到與其相鄰的點的另外一條路徑,多一條邊,而權值更小。或者可以理解為:每次加入新的節點i,將節點i作為中間節點,判斷源點—>節點i—>各個節點的最短距離 較之于 上一次的最短距離是否會有更新。那么我們只要對所有的點進行V-1次松弛操作,就可以求出從起點開始對任意一點的距離。如果還可以進行松弛操作,那么說明這個圖有負權環(如果有負權環,則可以進行無數次松弛操作)。
(雖然說是對i點進行松弛操作,但實際上是對i直接相鄰的點進行改變的)
例如:求1號結點到所有結點之間的距離[7]。
首先初始化數據結構,將dist數組的第0位置空(可以不用考慮),因為初始化數組dis的時候默認為頂點1還沒有邊相連,所以設置頂點1到其余各個頂點的距離均為∞。右表表示前一節點u,v,及其之間的權重w。
對第一輪的所有邊進行松弛。
松弛后的結果為:
由于這個案例比較特殊,只進行了一次就已經將所有的路徑都更新完畢了。但是更一般的情況,仍需要繼續松弛,整個松弛過程需要進行V-1次。
代碼實現:
#include
#include
using namespace std;
class Bellman_Ford
{
private:
int vertice = 0;//頂點數
int edge = 0;//邊數
vector u;
vector v;
vector w;
vector dis;//源點到各個頂點之間的最短距離
public:
//根據節點值和邊值初始化:邊的起始節點數組u,邊的終止節點數組v,邊u[i]->v[i]的權重w
Bellman_Ford(int x, int y) :vertice(x), edge(y)
{

//圖的初始化從下標1開始
dis.resize(vertice + 1);
u.resize(edge + 1);
v.resize(edge + 1);
w.resize(edge + 1);
}
//檢測負權回路
bool Detect_negative_weight_circuit()
{
bool flag = false;
for (int i = 1; i <= edge; i++)
{
if (dis[v[i]] > dis[u[i]] + w[i])
{
flag = 1;
}
}
return flag;
}
//讀入圖的邊,并且根據邊的信息初始化數組dis,數組book
void GetEdgeInfo()
{
cout << "輸入邊的信息(節點1,節點2,權重):" << endl;
int e1 = 0, e2 = 0, weigth = 0;
for (int i = 1; i <= edge; i++)
{
cin >> e1 >> e2 >> weigth;
u[i] = e1;
v[i] = e2;
w[i] = weigth;
}
for (int i = 2; i <= vertice; i++)
{
//dis[1]在構造函數里面已經初始化為0
dis[i] = INT_MAX;
}
}
//打印
void Print()

{
for (int i = 1; i <= vertice; i++)
{
cout << dis[i] << " ";
}
cout << endl;
}
//Bellman_Ford核心思想
void Bellman_Ford_Alg()
{
for (int k = 1; k < vertice; k++)//控制松弛的輪數
{
bool check = false;//標記在本輪松弛中數組dis是否會發送更新
//找離1號節點最近的節點(找數組dis中的最小值)
for (int i = 1; i <= edge; i++)
{
if (dis[u[i]] < INT_MAX && dis[v[i]] > (dis[u[i]] + w[i]))
{
dis[v[i]] = (dis[u[i]] + w[i]);
check = true;//如果數組dis發生變化,check的值就改變
}
}
//松弛結束后判斷dis數組是否發生變化
if (check == false)
{
break;
}
}
}
};
int main()
{
Bellman_Ford Bellman(5, 5);
Bellman.GetEdgeInfo();

cout << "初始信息:" << endl;
Bellman.Print();
Bellman.Bellman_Ford_Alg();
cout << "單源最短路徑(頂點1到其余各頂點):" << endl;
Bellman.Print();
bool tag = Bellman.Detect_negative_weight_circuit();
if (tag)
{
cout << "存在負權回路" << endl;
}
else
{
cout << "不存在負權回路" << endl;
}
return 0;
}
二、多源最短路徑
多源最短路徑是任意兩頂點之間的路徑。對于多源最短路徑,最經典的就是Floyd算法。Floyd算法又稱為插點法,是一種利用動態規劃的思想尋找給定的加權圖中多源點之間最短路徑的算法,需要不斷地松弛。
現在有這樣一張圖,每個點只知道與其直接相連的點的距離,將圖中的信息填入鄰接矩陣。并且將鄰接矩陣用二維數組dist[][]存儲起來。
加入第一個節點A進行更新計算,大家可以發現,由于A的加入,使得本來不連通的B,C點對和B,D點對變得聯通,并且加入A后距離為當前最小,同時你可以發現加入A其中也使得C-D多一條聯通路徑(6+3),但是C-D聯通的話距離為9遠遠大于本來的(C,D)聯通路徑2,所以這條不進行更新[8]。
加入第二個節點B
代碼演示:
參考文獻
1前k條最短路徑算法,嚴蔚敏、吳偉民:《數據結構(C語言版)》
2,最短路徑_百度百科 ()
3, 數據結構之圖的最短路徑_顧小豆的博客-CSDN博客_數據結構最短路徑
4,數據結構:圖(Graph)【詳解】的博客-CSDN博客_數據結構graph
5,【圖】最短路徑的類型總結_辰陽星宇的博客-CSDN博客
最短路徑_百度百科 ()
7, -Ford解決單源最短路徑(負權邊)_阿寧(xin)。的博客-CSDN博客_單源最短路徑 負邊8,(建議收藏)一文多圖,徹底搞懂Floyd算法(多源最短路徑)_Big sai的博客-CSDN博客_多源最短路徑